【题目】已知动圆![]() 过定点
过定点![]() ,且内切于定圆
,且内切于定圆![]() .
.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 方程;
方程;
(Ⅱ)在(Ⅰ)的条件下,记轨迹![]() 被
被![]() 所截得的弦长为
所截得的弦长为![]() ,求
,求![]() 的解析式及其最大值.
的解析式及其最大值.
参考答案:
【答案】(Ⅰ)点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为两焦点,长半轴为3的椭圆,方程为
为两焦点,长半轴为3的椭圆,方程为![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)根据题意设动圆![]() 的半径为
的半径为![]() ,则
,则![]() ,又动圆
,又动圆![]() 内切于定圆
内切于定圆![]() ,所以有
,所以有![]() ,所以
,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() 点轨迹是以
点轨迹是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,![]() ,
,![]() ,所以
,所以![]() ,所以轨迹方程为
,所以轨迹方程为![]() ;(Ⅱ)联立
;(Ⅱ)联立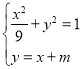 ,消去未知数
,消去未知数![]() 得:
得:![]() ,
,![]() ,解得
,解得![]() ,所以
,所以![]() ,设直线与椭圆交于
,设直线与椭圆交于![]() 两点,
两点,![]() ,
,![]() ,则弦长
,则弦长![]() ,所以有
,所以有![]() ,当
,当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
试题解析:(Ⅰ)设动圆圆心![]() ,动圆
,动圆![]() 半径为
半径为![]() ,
, ![]() ,
,
则![]() ,且
,且![]() ,则
,则![]() ,2分
,2分
即动圆圆心![]() 到两定点
到两定点![]() 和
和![]() 的距离之和恰好等于定圆半径6,
的距离之和恰好等于定圆半径6,
又![]() ,
,![]() ,
,
所以点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为两焦点,长半轴为3的椭圆.4分
为两焦点,长半轴为3的椭圆.4分
则![]() ,故求点的轨迹方程为:
,故求点的轨迹方程为:![]() .6分
.6分
(Ⅱ)联立方程组![]() ,消去
,消去![]() ,整理得
,整理得![]() 5分
5分
设交点坐标为![]() ,
,
则![]() ,解得
,解得![]() ,解得
,解得![]() 6分
6分
且 7分
7分
故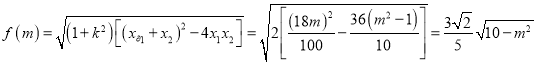 10分
10分
当![]() 时,弦长取得最大值为
时,弦长取得最大值为![]() .12分
.12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“三角形的内角中最多只有一个内角是钝角”时,应先假设( )
A. 没有一个内角是钝角 B. 有两个内角是钝角
C. 有三个内角是钝角 D. 至少有两个内角是钝角
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下程序运行后的输出结果为
i=1
WHILE i<8
i=i+2
S=2*i+3
i=i–1
WEND
PRINT S
END
A. 17 B. 19 C. 21 D. 23
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
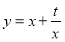 有如下性质:如果常数
有如下性质:如果常数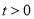 ,那么该函数在
,那么该函数在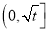 上是减函数,在
上是减函数,在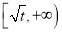 上是增函数.
上是增函数.(1)已知
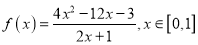 ,利用上述性质,求函数
,利用上述性质,求函数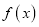 的单调区间和值域;
的单调区间和值域;(2)对于(1)中的函数
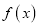 和函数
和函数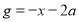 ,若对任意
,若对任意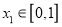 ,总存在
,总存在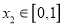 ,使得
,使得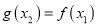 成立,求实数
成立,求实数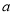 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算数平方根成正比,已知投资1万元时两类产品的收益分别是0.125万元和0.5万元(如图).
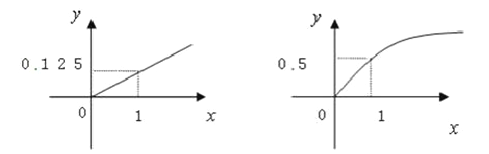
(1) 分别写出两种产品的收益与投资的函数关系;
(2) 该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:

(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,从这5人中再随机抽取3人赠送200元的护肤品套装,求这3人中“微信控”的人数为2的概率.
参考公式:
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.参考数据:

-
科目: 来源: 题型:
查看答案和解析>>【题目】分别求适合下列条件的双曲线的标准方程.
(Ⅰ)焦点在
 轴上,焦距是
轴上,焦距是 ,离心率
,离心率 ;
;(Ⅱ)一个焦点为
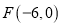 的等轴双曲线.
的等轴双曲线.
相关试题

