【题目】【2017唐山三模】已知函数![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在区间
在区间![]() 有唯一零点
有唯一零点![]() ,证明:
,证明: ![]() .
.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)求导得![]() , 分
, 分![]() ,
, ![]() ,
, ![]() ,三种情况讨论可得单调区间.
,三种情况讨论可得单调区间.
(Ⅱ)由(1)及![]() 可知:仅当极大值等于零,即
可知:仅当极大值等于零,即![]() 且
且 ![]()
所以![]() ,且
,且![]() ,消去
,消去![]() 得
得![]() ,构造函数,证明单调且零点存在且唯一即可.
,构造函数,证明单调且零点存在且唯一即可.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
若![]() ,即
,即![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
若![]() ,即
,即![]() ,则
,则![]() ,仅当
,仅当![]() 时,等号成立,
时,等号成立,
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
若![]() ,即
,即![]() ,则
,则![]() 有两个零点
有两个零点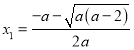 ,
, 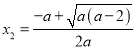 ,
,
由![]() ,
, ![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增.
单调递增.
综上所述,
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在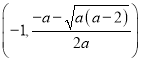 和
和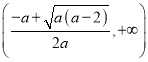 上单调递增,
上单调递增,
在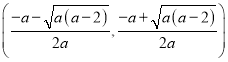 上单调递减.
上单调递减.
(Ⅱ)由(1)及![]() 可知:仅当极大值等于零,即
可知:仅当极大值等于零,即![]() 时,符合要求.
时,符合要求.
此时, ![]() 就是函数
就是函数![]() 在区间
在区间![]() 的唯一零点
的唯一零点![]() .
.
所以![]() ,从而有
,从而有![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
再由(1)知: ![]() ,
, ![]() ,
, ![]() 单调递减,
单调递减,
又因为![]() ,
, ![]() ,
,
所以![]() ,即
,即![]()
点晴:本题考查函数导数与单调性.确定零点的个数问题:可利用数形结合的办法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017衡阳第二次联考】已知函数
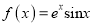 .
.(1)求函数
 的单调区间;
的单调区间;(2)如果对于任意的
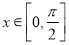 ,
,  恒成立,求实数
恒成立,求实数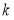 的取值范围;
的取值范围;(3)设函数
 ,
, 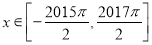 ,过点
,过点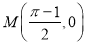 作函数
作函数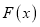 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列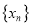 ,求数列
,求数列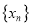 的所有项之和的值.
的所有项之和的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017省息一中第七次适应性考】已知函数
 (
(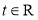 ),且
),且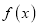 的导数为
的导数为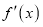 .
.(Ⅰ)若
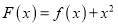 是定义域内的增函数,求实数
是定义域内的增函数,求实数 的取值范围;
的取值范围;(Ⅱ)若方程
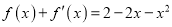 有3个不同的实数根,求实数
有3个不同的实数根,求实数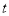 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义max{{x,y}=
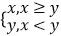 ,设f(x)=max{ax﹣a,﹣logax}(x∈R+ , a>0,a≠1).若a=
,设f(x)=max{ax﹣a,﹣logax}(x∈R+ , a>0,a≠1).若a=  ,则f(2)+f(
,则f(2)+f(  )=;若a>1,则不等式f(x)≥2的解集是
)=;若a>1,则不等式f(x)≥2的解集是 -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017锦州质量检测(二)】如图,在四棱锥
 中,底面
中,底面 为直角梯形,
为直角梯形,  ,
,  ,平面
,平面 底面
底面 ,
,  为
为 的中点,
的中点,  是棱
是棱 上的点,
上的点,  ,
,  .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)若三棱锥
 的体积是四棱锥
的体积是四棱锥 体积的
体积的 ,设
,设 ,试确定
,试确定 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
 的图象过点P(1,5).
的图象过点P(1,5).
(1)求实数m的值,并证明函数f(x)是奇函数;
(2)利用单调性定义证明f(x)在区间[2,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017衡阳第二次联考】已知四棱锥
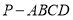 中,底面为矩形,
中,底面为矩形, 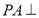 底面
底面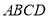 ,
, 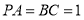 ,
, 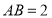 ,
, 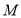 为
为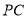 上一点,
上一点, 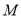 为
为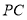 的中点.
的中点.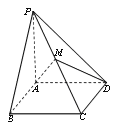
(1)在图中作出平面
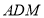 与
与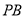 的交点
的交点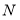 ,并指出点
,并指出点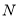 所在位置(不要求给出理由);
所在位置(不要求给出理由);(2)求平面
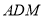 将四棱锥
将四棱锥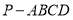 分成上下两部分的体积比.
分成上下两部分的体积比.
相关试题

