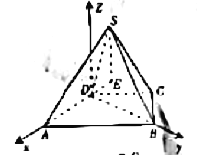
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,
是梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,侧面
,侧面![]() 底面
底面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1):取AB中点M,连接DM,可得DB⊥AD又侧面SAD⊥底面ABCD,可得BD⊥平面SAD,即可得平面SBD⊥平面SAD(2)以D为原点,DA,DB所在直线分别为x,y轴建立空间直角坐标系,求出设面SCB的法向量为: ![]() ,面SBD的法向量为
,面SBD的法向量为![]() .利用向量即可求解.
.利用向量即可求解.
解析:(1)因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() 是等腰直角三角形,
是等腰直角三角形,
故![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,
,
因为侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,
,
所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
因为侧面![]() 底面
底面![]() ,
,
所以![]() 底面
底面![]() ,
,
所以![]() 是底面
是底面![]() 与底面
与底面![]() 所成的角,即
所成的角,即![]() ,
,
过点![]() 在平面
在平面![]() 内作
内作![]() ,
,
因为侧面![]() 底面
底面![]() ,
,
所以![]() 底面
底面![]() ,
,
如图建立空间直角坐标系![]() ,
,
设![]() ,
, 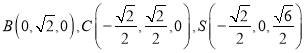 ,
,
则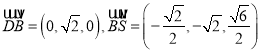 ,
, 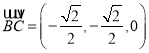 ,
,
设![]() 是平面
是平面![]() 法向量,
法向量,
则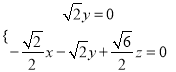
取![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则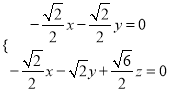
取![]() ,
, 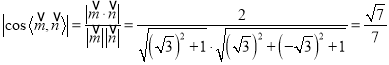
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别为a,b,c,且cosAcosC﹣cos(A+C)=sin2B. (Ⅰ)证明:a,b,c成等比数列;
(Ⅱ)若角B的平分线BD交AC于点D,且b=6,S△BAD=2S△BCD , 求BD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , a1=1,且(n+1)an=2Sn(n∈N*),数列{bn}满足
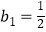 ,
, 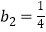 ,对任意n∈N* , 都有
,对任意n∈N* , 都有 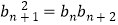 .
.
(1)求数列{an}、{bn}的通项公式;
(2)令Tn=a1b1+a2b2+…+anbn . 若对任意的n∈N* , 不等式λnTn+2bnSn<2(λn+3bn)恒成立,试求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,解不等式
,解不等式 ;
;(2)若存在实数
 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】以(a,1)为圆心,且与两直线x﹣y+1=0及x﹣y﹣3=0同时相切的圆的标准方程为( )
A.x2+(y﹣1)2=2
B.(x﹣2)2+(y﹣1)2=2
C.x2+(y﹣1)2=8
D.(x﹣2)2+(y﹣1)2=8 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下四个问题:①x,输出它的绝对值.②求面积为6的正方形的周长.③求三个数a,b,c中最大数.④求函数
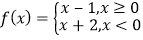 的函数值.其中不需要用条件语句来描述其算法的有 个.
的函数值.其中不需要用条件语句来描述其算法的有 个. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
A.
B.
C.
D.
相关试题

