【题目】设常数![]() .
.
(1)若![]() 在
在![]() 处取得极小值为
处取得极小值为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)对于任意给定的正实数![]() 、
、![]() ,证明:存在实数
,证明:存在实数![]() ,当
,当![]() 时,
时, ![]() .
.
参考答案:
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】试题分析:(1)本问考查极值点导数为,根据极值点导数为0,对函数求导, 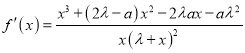 ,
, ![]() ,
, ![]() ,再根据
,再根据![]() ,可以求出
,可以求出![]() 的值;(2)本问考查存在性问题的证明,主要是将问题进行转化,
的值;(2)本问考查存在性问题的证明,主要是将问题进行转化, ![]() ,记
,记![]() ,故只需证明:存在实数
,故只需证明:存在实数![]() ,当
,当![]() 时,
时, ![]() ,而
,而 ![]() ,设
,设![]() ,通过证明得到恒有
,通过证明得到恒有![]() .即当
.即当![]() 时, 恒有
时, 恒有![]() 成立.
成立.
试题解析:(1)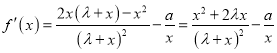
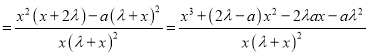 ,
,
∵![]() ,∴
,∴![]() .
.
将![]() 代入得
代入得
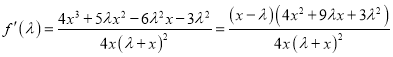
当![]() 时,
时, ![]() ,
, ![]() 递减;
递减;
![]() 时,
时, ![]() ,
, ![]() 递增;
递增;
故当![]() 时,
时, ![]() 取极小值
取极小值![]() ,
,
令![]() ,解得
,解得![]() .
.
(Ⅱ)因为![]() ,
,
记![]() ,故只需证明:存在实数
,故只需证明:存在实数![]() ,当
,当![]() 时,
时, ![]() ,
,
[方法1] ![]() ,
,
设![]() ,则
,则![]() .
.
易知当![]() 时,
时, ![]() ,故
,故![]() .
.
又由![]() 解得:
解得: ![]() ,即
,即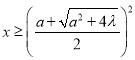
取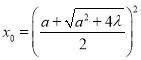 ,则当
,则当![]() 时, 恒有
时, 恒有![]() .
.
即当![]() 时, 恒有
时, 恒有![]() 成立.
成立.
[方法2] 由![]() ,得:
,得: ![]() ,
,
故![]() 是区间
是区间![]() 上的增函数.令
上的增函数.令![]() ,
,
则![]() ,因为
,因为![]() ,
,
故有![]() ,
,
令![]() ,解得:
,解得: 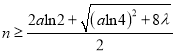 ,
,
设![]() 是满足上述条件的最小正整数,取
是满足上述条件的最小正整数,取![]() ,则当
,则当![]() 时, 恒有
时, 恒有![]() ,
,
即![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于给定的正整数k,若数列lanl 满足

=2kan对任意正整数n(n> k) 总成立,则称数列lanl 是“P(k)数列”.学科@网
(1)证明:等差数列lanl是“P(3)数列”;
若数列lanl既是“P(2)数列”,又是“P(3)数列”,证明:lanl是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列an的首项a1=2,且an=2an﹣1﹣1(nN+ , n≥2).
(1)求数列{an}的通项公式;
(2)求数列{nan﹣n}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的各项都为正数,其前n项和为Sn , 已知4Sn=an2+2an .
(1)求a1级数列{an}的通项公式;
(2)设数列{bn}前n项和为Tn , 且bn=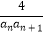 ,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围.
,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x),将f(x)图像沿x轴向右平移
 个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣
个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣  )的图像相同,那么y=f(x)的解析式为( )
)的图像相同,那么y=f(x)的解析式为( )
A.f(x)=2sin(2x﹣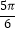 )
)
B.f(x)=2sin(2x﹣ )
)
C.f(x)=2sin(2x+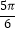 )
)
D.f(x)=2sin(2x+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】平面内给定三个向量
 =(3,2),
=(3,2), 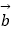 =(﹣1,2),
=(﹣1,2),  =(4,1).回答下列问题:
=(4,1).回答下列问题:
(1)若( +k
+k  )∥(2
)∥(2 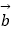 ﹣
﹣  ),求实数k;
),求实数k;
(2)设 =(x,y)满足(
=(x,y)满足(  ﹣
﹣  )∥(
)∥(  +
+ 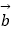 )且|
)且|  ﹣
﹣  |=1,求
|=1,求  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的偶函数f(x)满足对于任意实数x,都有f(1+x)=f(1﹣x),且当0≤x≤1时,f(x)=3x+1 .
(1)求证:函数f(x)是周期函数;
(2)当x∈[1,3]时,求f(x)的解析式.
相关试题

