【题目】对于给定的正整数k,若数列lanl 满足![]()
=2kan对任意正整数n(n> k) 总成立,则称数列lanl 是“P(k)数列”.学科@网
(1)证明:等差数列lanl是“P(3)数列”;
若数列lanl既是“P(2)数列”,又是“P(3)数列”,证明:lanl是等差数列.
参考答案:
【答案】当{an}为等差数列时,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]() (
(![]() ,
,![]() ),
),
![]() (
(![]() ,
,![]() ),
),
∴![]() ,∴
,∴![]() ,
,
∴数列{an}是等差数列.
【解析】
证明:(1)因为![]() 是等差数列,设其公差为
是等差数列,设其公差为![]() ,则
,则![]() ,
,
从而,当![]() 时,
时,![]()
![]()
![]() ,
,![]()
所以![]() ,
,
因此等差数列![]() 是“
是“![]() 数列”.
数列”.
(2)数列![]() 既是“
既是“![]() 数列”,又是“
数列”,又是“![]() 数列”,因此,
数列”,因此,
当![]() 时,
时,![]() ,①
,①
当![]() 时,
时,![]() .②
.②
由①知,![]()
![]() ,③
,③
![]()
![]() ,④
,④
将③④代入②,得![]() ,其中
,其中![]() ,
,
所以![]() 是等差数列,设其公差为
是等差数列,设其公差为![]() .
.
在①中,取![]() ,则
,则![]() ,所以
,所以![]() ,
,
在①中,取![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以数列![]() 是等差数列.
是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).
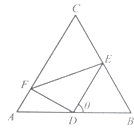
(1)当tan∠DEF=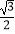 时,求θ的大小;
时,求θ的大小;
(2)求△DEF的面积S的最小值及使得S取最小值时θ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输入S的值为﹣1,则输出S的值为( )

A.﹣1
B.
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
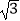 sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,
sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,  ]上的最大值和最小值;
]上的最大值和最小值;
(Ⅱ)若f(x0)=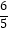 ,x0∈[
,x0∈[  ,
,  ],求cos2x0的值.
],求cos2x0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列an的首项a1=2,且an=2an﹣1﹣1(nN+ , n≥2).
(1)求数列{an}的通项公式;
(2)求数列{nan﹣n}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的各项都为正数,其前n项和为Sn , 已知4Sn=an2+2an .
(1)求a1级数列{an}的通项公式;
(2)设数列{bn}前n项和为Tn , 且bn=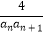 ,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围.
,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设常数
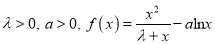 .
.(1)若
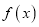 在
在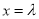 处取得极小值为
处取得极小值为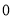 ,求
,求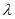 和
和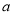 的值;
的值;(2)对于任意给定的正实数
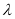 、
、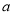 ,证明:存在实数
,证明:存在实数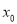 ,当
,当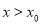 时,
时, 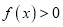 .
.
相关试题

