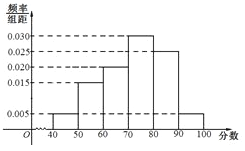
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考答案:
【答案】(1)平均分![]() ,众数
,众数![]() 分;(2)分布列见解析,期望
分;(2)分布列见解析,期望![]() .
.
【解析】试题分析:(1)利用中值估算抽样学生的平均分;(2)求出两个数恰好是两个学生的数学成绩的概率,确定随机变量![]() 的可能取值,求出相应的概率,可求
的可能取值,求出相应的概率,可求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
试题解析:(1)平均分![]()
![]()
![]() 分.
分.
众数的估计值是75分.
(2)在![]() 段的人数
段的人数![]() (人),
(人),
设每次抽取两个数恰好是两名学生的成绩的概率为![]() ,则
,则![]() ,
,
显然, ![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3. ![]() ,
, ![]()
![]()
![]()
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  。
。(1)写出
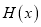 的解析式与定义域;
的解析式与定义域;(2)画出函数
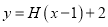 的图像;
的图像;(3)试讨论方程
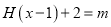 的根的个数。
的根的个数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
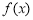 是单调减函数,若将方程
是单调减函数,若将方程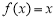 与
与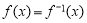 的解分别称为函数
的解分别称为函数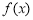 的不动点与稳定点.则“
的不动点与稳定点.则“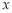 是
是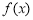 的不动点”是“
的不动点”是“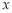 是
是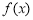 的稳定点”的 ( )
的稳定点”的 ( )A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资
 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.(1)分别写出
 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
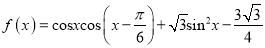 .
.(1)求
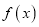 的最小正周期
的最小正周期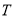 ;
;(2)设
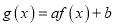 ,若
,若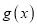 在
在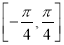 上的值域为
上的值域为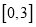 ,求实数
,求实数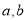 的值;
的值;(3)若
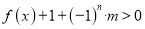 对任意的
对任意的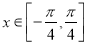 和
和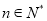 恒成立,求实数
恒成立,求实数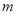 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
-
科目: 来源: 题型:
查看答案和解析>>【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表:
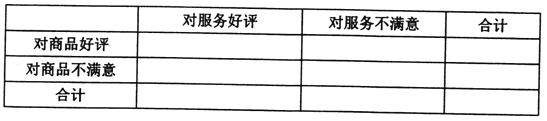
(2)通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;

相关试题

