【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量 ![]() =(2sinA,cos(A﹣B)),
=(2sinA,cos(A﹣B)), ![]() =(sinB,﹣1),且
=(sinB,﹣1),且 ![]()
![]() =
= ![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ![]() ,求b﹣a的取值范围.
,求b﹣a的取值范围.
参考答案:
【答案】解:(Ⅰ)由 ![]()
![]() =
= ![]() ,得
,得 ![]() ,
, ![]() ,
,
∴ ![]() ,即
,即 ![]() ,
,
∵0<C<π,
∴ ![]() .
.
(Ⅱ)∵ ![]() ,且
,且 ![]() ,
,
∴  ,
,
∴a=2sinA,b=2sinB.
∴b﹣a=2sinB﹣2sinA= ![]()
= ![]() =
= ![]()
= ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]()
【解析】(Ⅰ)由 ![]()
![]() =
= ![]() ,得
,得 ![]() ,化简可得
,化简可得 ![]() ,结合范围0<C<π,即可求C的值.(Ⅱ)由正弦定理可得a=2sinA,b=2sinB.从而可得b﹣a=
,结合范围0<C<π,即可求C的值.(Ⅱ)由正弦定理可得a=2sinA,b=2sinB.从而可得b﹣a= ![]() ,由
,由 ![]() ,可得 /span>
,可得 /span>![]() ,利用余弦函数的图象和性质即可解得b﹣a的范围.
,利用余弦函数的图象和性质即可解得b﹣a的范围.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
 的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
(1)若l的倾斜角为 ,
,  是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,过椭圆M:
 (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣  =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为  .
.
(1)求M的方程
(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中, 平面
中, 平面 平面
平面 ,
, .
.
(1)求证:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)在棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在, 求
?若存在, 求 的值;若不存在, 说明理由.
的值;若不存在, 说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出一个问题的算法:
S1 输入x;
S2 若x≤2,则执行S3;否则,执行S4;
S3 输出-2x-1;
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形,  平面
平面 ,点
,点 ,
,  分别为
分别为 ,
,  的中点,且
的中点,且 ,
,  .
.
(1)证明:
 平面
平面 ;
;(2)设直线
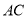 与平面
与平面 所成角为
所成角为 ,当
,当 在
在 内变化时,求二面角
内变化时,求二面角 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)将函数
 的图象向右平移
的图象向右平移 个单位长度,再向下平移
个单位长度,再向下平移 (
( )个单位长度后得到函数
)个单位长度后得到函数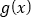 的图象,且函数
的图象,且函数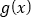 的最大值为2.
的最大值为2.(ⅰ)求函数
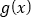 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数
的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数 ,使得
,使得 .
.
相关试题

