【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 的图象,且函数
的图象,且函数![]() 的最大值为2.
的最大值为2.
(ⅰ)求函数![]() 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数
的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数![]() ,使得
,使得![]() .
.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(Ⅰ)因为![]()
![]()
![]() .
.
所以函数![]() 的最小正周期
的最小正周期![]() .
.
(Ⅱ)(Ⅰ)将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到
个单位长度后得到![]() 的图象,再向下平移
的图象,再向下平移![]() (
(![]() )个单位长度后得到
)个单位长度后得到![]() 的图象.
的图象.
又已知函数![]() 的最大值为
的最大值为![]() ,所以
,所以![]() ,解得
,解得![]() .
.
所以![]() .
.
(Ⅱ)要证明存在无穷多个互不相同的正整数![]() ,使得
,使得![]() ,就是要证明存在无穷多个互不相同的正整数
,就是要证明存在无穷多个互不相同的正整数![]() ,使得
,使得![]() ,即
,即![]() .
.
由![]() 知,存在
知,存在![]() ,使得
,使得![]() .
.
由正弦函数的性质可知,当![]() 时,均有
时,均有![]() .
.
因为![]() 的周期为
的周期为![]() ,
,
所以当![]() (
(![]() )时,均有
)时,均有![]() .
.
因为对任意的整数![]() ,
,![]() ,
,
所以对任意的正整数![]() ,都存在正整数
,都存在正整数![]() ,使得
,使得![]() .
.
亦即存在无穷多个互不相同的正整数![]() ,使得
,使得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量
 =(2sinA,cos(A﹣B)),
=(2sinA,cos(A﹣B)),  =(sinB,﹣1),且
=(sinB,﹣1),且 
 =
=  .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ,求b﹣a的取值范围.
,求b﹣a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出一个问题的算法:
S1 输入x;
S2 若x≤2,则执行S3;否则,执行S4;
S3 输出-2x-1;
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形,  平面
平面 ,点
,点 ,
,  分别为
分别为 ,
,  的中点,且
的中点,且 ,
,  .
.
(1)证明:
 平面
平面 ;
;(2)设直线
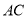 与平面
与平面 所成角为
所成角为 ,当
,当 在
在 内变化时,求二面角
内变化时,求二面角 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学利用春节进行社会实践,对本地
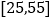 岁的人群随机抽取
岁的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图。
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图。
(一)人数统计表: (二)各年龄段人数频率分布直方图:
(Ⅰ)在答题卡给定的坐标系中补全频率分布直方图,并求出
 、
、 、
、 的值;
的值;(Ⅱ)从
 岁年龄段的“低碳族”中采用分层抽样法抽取
岁年龄段的“低碳族”中采用分层抽样法抽取 人参加户外低碳体验活动。若将这
人参加户外低碳体验活动。若将这 个人通过抽签分成甲、乙两组,每组的人数相同,求
个人通过抽签分成甲、乙两组,每组的人数相同,求 岁中被抽取的人恰好又分在同一组的概率。
岁中被抽取的人恰好又分在同一组的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,F1 , F2分别为椭圆
 +
+ 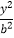 =1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. 
(1)若点C的坐标为( ,
,  ),且BF2=
),且BF2=  ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在圆
 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足.
为垂足. ,当点
,当点 在圆上运动时,
在圆上运动时,(1)求
 点的轨迹
点的轨迹 的方程;
的方程;(2) 若
 ,直线
,直线 交曲线
交曲线 于
于 、
、 两点(点
两点(点 、
、 与点
与点 不重合),且满足
不重合),且满足 .
.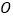 为坐标原点,点
为坐标原点,点 满足
满足 ,证明直线
,证明直线 过定点,并求直线
过定点,并求直线 的斜率的取值范围.
的斜率的取值范围.
相关试题

