【题目】如图,在四棱锥![]() 中, 平面
中, 平面![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在, 求
?若存在, 求![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】试题分析:(Ⅰ)由面面垂直的性质定理知AB⊥平面![]() ,根据线面垂直的性质定理可知
,根据线面垂直的性质定理可知![]() ,再由线面垂直的判定定理可知
,再由线面垂直的判定定理可知![]() 平面
平面![]() ;(Ⅱ)取
;(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,以O为坐标原点建立空间直角坐标系O-xyz,利用向量法可求出直线PB与平面PCD所成角的正弦值;(Ⅲ)假设存在,根据A,P,M三点共线,设
,以O为坐标原点建立空间直角坐标系O-xyz,利用向量法可求出直线PB与平面PCD所成角的正弦值;(Ⅲ)假设存在,根据A,P,M三点共线,设![]() ,根据BM∥平面PCD,即
,根据BM∥平面PCD,即![]() (
(![]() 为平面PCD的法向量),求出
为平面PCD的法向量),求出![]() 的值,从而求出
的值,从而求出![]() 的值.
的值.
试题解析:(Ⅰ)因为平面![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]() .
.
又因为![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() .
.
因为![]() ,所以
,所以![]() .
.
如图建立空间直角坐标系![]() .由题意得,
.由题意得,
![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
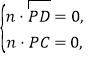 即
即![]()
令![]() ,则
,则![]() .
.
所以![]() .
.
又![]() ,所以
,所以![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
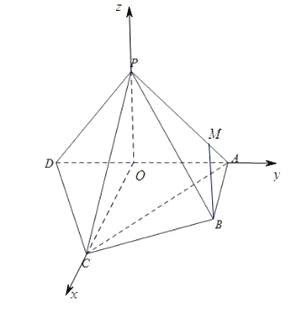
(Ⅲ)设![]() 是棱
是棱![]() 上一点,则存在
上一点,则存在![]() 使得
使得![]() .
.
因此点![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() 当且仅当
当且仅当![]() ,
,
即![]() ,解得
,解得![]() .
.
所以在棱![]() 上存在点
上存在点![]() 使得
使得![]() 平面
平面![]() ,此时
,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=4x,焦点为F,过点P(﹣1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若
 +
+ 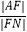 =18,则k= .
=18,则k= . -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
 的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
(1)若l的倾斜角为 ,
,  是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,过椭圆M:
 (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣  =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为  .
.
(1)求M的方程
(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量
 =(2sinA,cos(A﹣B)),
=(2sinA,cos(A﹣B)),  =(sinB,﹣1),且
=(sinB,﹣1),且 
 =
=  .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ,求b﹣a的取值范围.
,求b﹣a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出一个问题的算法:
S1 输入x;
S2 若x≤2,则执行S3;否则,执行S4;
S3 输出-2x-1;
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形,  平面
平面 ,点
,点 ,
,  分别为
分别为 ,
,  的中点,且
的中点,且 ,
,  .
.
(1)证明:
 平面
平面 ;
;(2)设直线
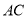 与平面
与平面 所成角为
所成角为 ,当
,当 在
在 内变化时,求二面角
内变化时,求二面角 的取值范围.
的取值范围.
相关试题

