【题目】平面直角坐标系xOy中,过椭圆M: ![]() (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣ ![]() =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为 ![]() .
.
(1)求M的方程
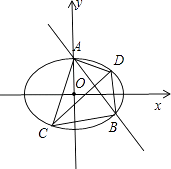
(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
参考答案:
【答案】
(1)解:把右焦点(c,0)代入直线x+y﹣ ![]() =0得c+0﹣
=0得c+0﹣ ![]() =0,解得c=
=0,解得c= ![]() .
.
设A(x1,y1),B(x2,y2),线段AB的中点P(x0,y0),
则 ![]() ,
, ![]() ,相减得
,相减得 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,又
,又 ![]() =
= ![]() ,
,
∴ ![]() ,即a2=2b2.
,即a2=2b2.
联立得 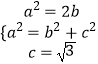 ,解得
,解得 ![]() ,
,
∴M的方程为 ![]() .
.
(2)解:∵CD⊥AB,∴可设直线CD的方程为y=x+t,
联立 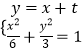 ,消去y得到3x2+4tx+2t2﹣6=0,
,消去y得到3x2+4tx+2t2﹣6=0,
∵直线CD与椭圆有两个不同的交点,
∴△=16t2﹣12(2t2﹣6)=72﹣8t2>0,解﹣3<t<3(*).
设C(x3,y3),D(x4,y4),∴ ![]() ,
, ![]() .
.
∴|CD|= ![]() =
= ![]() =
= ![]() .
.
联立 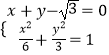 得到3x2﹣4
得到3x2﹣4 ![]() x=0,解得x=0或
x=0,解得x=0或 ![]() ,
,
∴交点为A(0, ![]() ),B
),B ![]() ,
,
∴|AB|= ![]() =
= ![]() .
.
∴S四边形ACBD= ![]() =
= ![]() =
= ![]() ,
,
∴当且仅当t=0时,四边形ACBD面积的最大值为 ![]() ,满足(*).
,满足(*).
∴四边形ACBD面积的最大值为 ![]() .
.
【解析】(1)把右焦点(c,0)代入直线可解得c.设A(x1 , y1),B(x2 , y2),线段AB的中点P(x0 , y0),利用“点差法”即可得到a,b的关系式,再与a2=b2+c2联立即可得到a,b,c.(2)由CD⊥AB,可设直线CD的方程为y=x+t,与椭圆的方程联立得到根与系数的关系,即可得到弦长|CD|.把直线x+y﹣ ![]() =0与椭圆的方程联立得到根与系数的关系,即可得到弦长|AB|,利用S四边形ACBD=
=0与椭圆的方程联立得到根与系数的关系,即可得到弦长|AB|,利用S四边形ACBD= ![]() 即可得到关于t的表达式,利用二次函数的单调性即可得到其最大值.
即可得到关于t的表达式,利用二次函数的单调性即可得到其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶图如图所示:

(Ⅰ)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(Ⅱ)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中地理成绩;
(Ⅲ)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=4x,焦点为F,过点P(﹣1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若
 +
+ 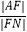 =18,则k= .
=18,则k= . -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
 的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
(1)若l的倾斜角为 ,
,  是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中, 平面
中, 平面 平面
平面 ,
, .
.
(1)求证:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)在棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在, 求
?若存在, 求 的值;若不存在, 说明理由.
的值;若不存在, 说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量
 =(2sinA,cos(A﹣B)),
=(2sinA,cos(A﹣B)),  =(sinB,﹣1),且
=(sinB,﹣1),且 
 =
=  .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ,求b﹣a的取值范围.
,求b﹣a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出一个问题的算法:
S1 输入x;
S2 若x≤2,则执行S3;否则,执行S4;
S3 输出-2x-1;
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
相关试题

