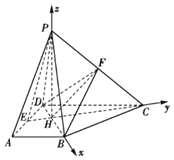
【题目】如图所示,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,点E为AD的中点,
,点E为AD的中点,![]() ,
,![]() 平面ABCD,且
平面ABCD,且![]()

(1)求证:![]() ;
;
(2)线段PC上是否存在一点F,使二面角![]() 的余弦值是
的余弦值是![]() ?若存在,请找出点F的位置;若不存在,请说明理由.
?若存在,请找出点F的位置;若不存在,请说明理由.
参考答案:
【答案】(1)见证明;(2)见解析
【解析】
(1)由题意,证得![]() ,再由线面垂直的性质,证得
,再由线面垂直的性质,证得![]() ,利用线面垂直的判定定理,即可证得
,利用线面垂直的判定定理,即可证得![]() 平面PEC,进而得到
平面PEC,进而得到![]() .
.
(2)由(1)建立以H为坐标原点,HB、HC、HP所在直线分别为x,y,z轴的坐标系,由![]() 与
与![]() 共线,得
共线,得![]() ,再求得平面CPD和平面CPD的一个法向量,利用向量的夹角公式即可求解.
,再求得平面CPD和平面CPD的一个法向量,利用向量的夹角公式即可求解.
证明:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
E为AD的中点,![]() ,
,
![]() ≌
≌![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,![]() ,
,
又![]() ,且PH,
,且PH,![]() 平面PEC,
平面PEC,![]() 平面PEC,
平面PEC,
又![]() 平面PEC,
平面PEC,![]() .
.
解:(2)由(1)可知![]() ∽
∽![]() ,
,
由题意得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 、EC、BD两两垂直,建立以H为坐标原点,HB、HC、HP所在直线分别为x,y,z轴的坐标系,
、EC、BD两两垂直,建立以H为坐标原点,HB、HC、HP所在直线分别为x,y,z轴的坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
假设线段PC上存在一点F满足题意,
![]() 与
与![]() 共线,
共线,
∴存在唯一实数![]() ,
,![]() ,满足
,满足![]() ,解得
,解得![]() ,
,
设向量![]() 为平面CPD的一个法向量,
为平面CPD的一个法向量,
且![]() ,
,![]() ,
,
∴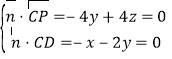 ,取
,取![]() ,得
,得![]() ,
,
同理得平面CPD的一个法向量![]() ,
,
∵二面角![]() 的余弦值是
的余弦值是![]() ,
,
∴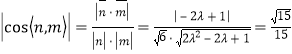 ,
,
由![]() ,解得
,解得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,△ABC和△AA1C均是边长为2的等边三角形,点O为AC中点,平面AA1C1C⊥平面ABC.

(1)证明:A1O⊥平面ABC;
(2)求直线AB与平面A1BC1所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆
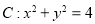 与
与 轴的左右交点分别为
轴的左右交点分别为 ,与
,与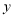 轴正半轴的交点为
轴正半轴的交点为 .
.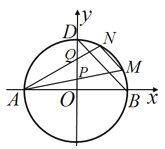
(1)若直线
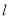 过点
过点 并且与圆
并且与圆 相切,求直线
相切,求直线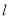 的方程;
的方程;(2)若点
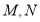 是圆
是圆 上第一象限内的点,直线
上第一象限内的点,直线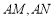 分别与
分别与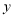 轴交于点
轴交于点 ,点
,点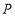 是线段
是线段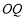 的中点,直线
的中点,直线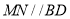 ,求直线
,求直线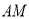 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=
 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 :
: 和二次函数
和二次函数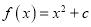 ,若直线
,若直线 与二次函数
与二次函数 的图象交于
的图象交于 ,
, 两点.
两点.(1)求直线
 在
在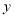 轴上的截距
轴上的截距 ;
;(2)若点
 的坐标为
的坐标为 ,求
,求 点的坐标;
点的坐标;(3)当
 时,是否存在直线
时,是否存在直线 与圆
与圆 :
: 相切?若存在,求线段
相切?若存在,求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
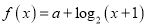 ,且
,且 .
.(1)求实数
 的值,并指出函数
的值,并指出函数 的定义域;
的定义域;(2)将函数
 图象上的所有点向右平行移动1个单位得到函数
图象上的所有点向右平行移动1个单位得到函数 的图象,写出函数
的图象,写出函数 的表达式;
的表达式;(3)对于(2)中的
 ,关于
,关于 的函数
的函数 在
在 上的最小值为2,求
上的最小值为2,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的离心率为
的离心率为 ,左顶点到直线
,左顶点到直线 的距离为
的距离为 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线
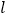 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
相关试题

