【题目】已知函数![]() ,且
,且![]() .
.
(1)求实数![]() 的值,并指出函数
的值,并指出函数![]() 的定义域;
的定义域;
(2)将函数![]() 图象上的所有点向右平行移动1个单位得到函数
图象上的所有点向右平行移动1个单位得到函数![]() 的图象,写出函数
的图象,写出函数![]() 的表达式;
的表达式;
(3)对于(2)中的![]() ,关于
,关于![]() 的函数
的函数![]() 在
在![]() 上的最小值为2,求
上的最小值为2,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;定义域
;定义域![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据![]() ,结合对数运算,即可求得参数;由真数大于零,即可求得定义域.
,结合对数运算,即可求得参数;由真数大于零,即可求得定义域.
(2)根据左加右减的平移原则,即可容易求得;
(3)利用换元法,将问题转化为求二次函数最小值的问题,根据动轴定区间问题的处理方式,分类讨论即可.
(1)因为![]() ,且
,且![]() ,
,
故可得![]() ,解得
,解得![]() .
.
故![]() ,要使得函数有意义,
,要使得函数有意义,
则![]() ,解得
,解得![]() ,
,
故函数![]() 的定义域为
的定义域为![]() .
.
(2)![]() 图象上的所有点向右平行移动1个单位得到函数
图象上的所有点向右平行移动1个单位得到函数![]() 的图象,
的图象,
又因为![]() ,
,
故可得![]() .
.
(3)由(2)可知![]() ,
,
故![]() 等价于:
等价于:
![]() ,
,
令![]() ,则
,则![]()
则![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
又因为其对称轴为![]() ,
,
①当![]() 时,二次函数在
时,二次函数在![]() 上单调递增,
上单调递增,
故![]() ,不符合题意,故舍去;
,不符合题意,故舍去;
②当![]() 时,二次函数在
时,二次函数在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故![]() ,解得
,解得![]() ,
,
故此时满足题意的![]() ;
;
③当![]() 时,二次函数在
时,二次函数在![]() 上单调递减,
上单调递减,
故![]() ,解得
,解得![]() ,故舍去.
,故舍去.
综上所述:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=
 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形, ,
, ,
, ,点E为AD的中点,
,点E为AD的中点, ,
, 平面ABCD,且
平面ABCD,且

(1)求证:
 ;
;(2)线段PC上是否存在一点F,使二面角
 的余弦值是
的余弦值是 ?若存在,请找出点F的位置;若不存在,请说明理由.
?若存在,请找出点F的位置;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 :
: 和二次函数
和二次函数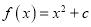 ,若直线
,若直线 与二次函数
与二次函数 的图象交于
的图象交于 ,
, 两点.
两点.(1)求直线
 在
在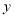 轴上的截距
轴上的截距 ;
;(2)若点
 的坐标为
的坐标为 ,求
,求 点的坐标;
点的坐标;(3)当
 时,是否存在直线
时,是否存在直线 与圆
与圆 :
: 相切?若存在,求线段
相切?若存在,求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的离心率为
的离心率为 ,左顶点到直线
,左顶点到直线 的距离为
的距离为 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线
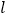 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设F为抛物线
 的焦点,A,B,C为该抛物线上三点,若
的焦点,A,B,C为该抛物线上三点,若 ,则
,则 = ( )
= ( )A. 9 B. 6 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线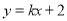 与E交于A、B两点,且
与E交于A、B两点,且 ,其中O为原点.
,其中O为原点.(1)求抛物线E的方程;
(2)点C坐标为
 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为 ,证明:
,证明:  为定值.
为定值.
相关试题

