【题目】如图,已知圆![]() 与
与![]() 轴的左右交点分别为
轴的左右交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() .
.
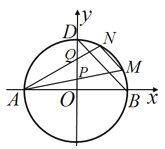
(1)若直线![]() 过点
过点![]() 并且与圆
并且与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 上第一象限内的点,直线
上第一象限内的点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() ,求直线
,求直线![]() 的斜率.
的斜率.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先验证当直线斜率不存在时,可知满足题意;当直线斜率不存在时,假设直线方程,利用![]() 构造方程可求得切线斜率,从而得到结果;(2)假设直线
构造方程可求得切线斜率,从而得到结果;(2)假设直线![]() 方程,与圆的方程联立可求得
方程,与圆的方程联立可求得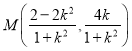 ;求出直线
;求出直线![]() 斜率后,可得
斜率后,可得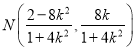 ,利用
,利用![]() 可知
可知![]() ,从而构造方程可求得直线
,从而构造方程可求得直线![]() 的斜率.
的斜率.
(1)当斜率不存在时,直线方程为:![]() ,与圆相切,满足题意
,与圆相切,满足题意
当斜率存在时,设切线方程为:![]() ,即:
,即:![]()
由直线与圆相切得:![]() ,即:
,即:![]() ,解得:
,解得:![]()
![]() 切线方程为:
切线方程为:![]() ,即:
,即:![]()
综上所述,切线方程为:![]() 或
或![]()
(2)由题意易知直线![]() 的斜率存在
的斜率存在
故设直线![]() 的方程为:
的方程为:![]() ,
,![]()
由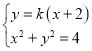 消去
消去![]() 得:
得:![]()
![]()
![]() ,代入
,代入![]() 得:
得:![]()
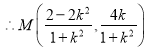
在![]() 中,令
中,令![]() 得:
得:![]()
![]() 点
点![]() 是线段
是线段![]() 的中点
的中点 ![]()
![]()
在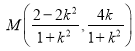 中,用
中,用![]() 代
代![]() 得:
得: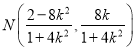
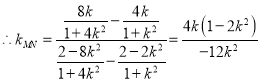
![]() 且
且![]()
![]()
即:![]() ,又
,又![]() ,解得:
,解得:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知递减等差数列{an}满足:a1=2,a2a3=40. (Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)若递减等比数列{bn}满足:b2=a2 , b4=a4 , 求数列{bn}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=axex , 其中常数a≠0,e为自然对数的底数. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当a=1时,求函数f(x)的极值;
(Ⅲ)若直线y=e(x﹣ )是曲线y=f(x)的切线,求实数a的值.
)是曲线y=f(x)的切线,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD的中点,PE⊥BE,PA=PD=AD=2,AB=
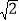 .
.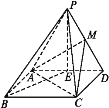
(1)求证:PB∥平面MAC.
(2)求证:平面MAC⊥平面PBE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面凸四边形
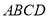 中(凸四边形指没有角度数大于
中(凸四边形指没有角度数大于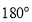 的四边形),
的四边形),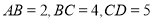 .
.
(1)若
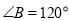 ,
,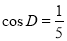 ,求
,求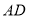 ;
;(2)已知
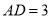 ,记四边形
,记四边形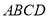 的面积为
的面积为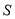 .
.① 求
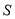 的最大值;
的最大值;② 若对于常数
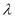 ,不等式
,不等式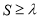 恒成立,求实数
恒成立,求实数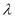 的取值范围.(直接写结果,不需要过程)
的取值范围.(直接写结果,不需要过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 +
+  =1(a>b>0),离心率e=
=1(a>b>0),离心率e=  ,已知点P(0,
,已知点P(0,  )到椭圆C的右焦点F的距离是
)到椭圆C的右焦点F的距离是  .设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
.设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)求点Q的横坐标x0的取值范围.
相关试题

