【题目】如图,在三棱柱ABC-A1B1C1中,△ABC和△AA1C均是边长为2的等边三角形,点O为AC中点,平面AA1C1C⊥平面ABC.

(1)证明:A1O⊥平面ABC;
(2)求直线AB与平面A1BC1所成角的正弦值.
参考答案:
【答案】(1)见证明;(2)![]()
【解析】
(1)由AA1=A1C,且O为AC的中点,得A1O⊥AC,根据面面垂直的性质定理,即可证得A1O⊥平面ABC;
(2)以O为原点,OB,OC,OA1为x,y,z轴,建立空间直角坐标系,求得平面A1BC1的一个法向量,利用向量的夹角公式,即可求解.
(1)证明:∵AA1=A1C,且O为AC的中点,
∴A1O⊥AC,
又∵平面AA1C1C⊥平面ABC,且交线为AC,又A1O平面AA1C1C,
∴A1O⊥平面ABC;
(2)如图,以O为原点,OB,OC,OA1为x,y,z轴,建立空间直角坐标系.
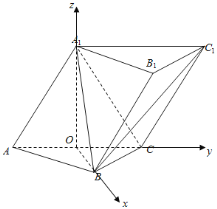
由已知可得O(0,0,0)A(0,-1,0)![]() ,
,
![]() ,
,![]()
平面A1BC1的法向量为![]() ,
,
则有![]() ,
,
所以![]() 的一组解为
的一组解为![]() ,
,
设直线AB与平面A1BC1所成角为![]() ,
,
则![]()
又∵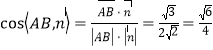 ,
,
所以直线AB与平面A1BC1所成角的正弦值:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2017年1月18日开始,支付宝用户可以通过“
 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表: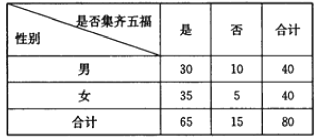
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式:
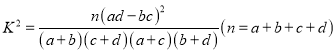 .
.附表:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下五个关于圆锥曲线的命题中:
①平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹为
 ;
;②点P是抛物线
 上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则
上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则 的最小值是6;
的最小值是6;③平面内到两定点距离之比等于常数
 的点的轨迹是圆;
的点的轨迹是圆;④若过点C(1,1)的直线
 交椭圆
交椭圆 于不同的两点A,B,且C是AB的中点,则直线
于不同的两点A,B,且C是AB的中点,则直线 的方程是
的方程是 .
.⑤已知P为抛物线
 上一个动点,Q为圆
上一个动点,Q为圆 上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
其中真命题的序号是______.(写出所有真命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆
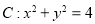 与
与 轴的左右交点分别为
轴的左右交点分别为 ,与
,与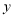 轴正半轴的交点为
轴正半轴的交点为 .
.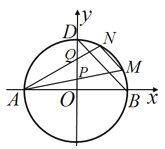
(1)若直线
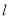 过点
过点 并且与圆
并且与圆 相切,求直线
相切,求直线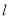 的方程;
的方程;(2)若点
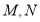 是圆
是圆 上第一象限内的点,直线
上第一象限内的点,直线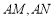 分别与
分别与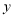 轴交于点
轴交于点 ,点
,点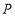 是线段
是线段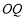 的中点,直线
的中点,直线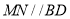 ,求直线
,求直线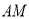 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=
 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形, ,
, ,
, ,点E为AD的中点,
,点E为AD的中点, ,
, 平面ABCD,且
平面ABCD,且

(1)求证:
 ;
;(2)线段PC上是否存在一点F,使二面角
 的余弦值是
的余弦值是 ?若存在,请找出点F的位置;若不存在,请说明理由.
?若存在,请找出点F的位置;若不存在,请说明理由.
相关试题

