【题目】如图,在四棱锥P﹣ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB 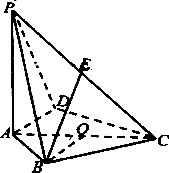
(1)求证:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值为2,求直线PB与平面PCD所成角的正弦值.
参考答案:
【答案】
(1)证明:∵,∠DAC=∠AOB
∴AD∥OB,
∵E是PC的中点,O是AC的中点,
∴OE是△PAC的中位线,
∴OE∥PA,
∵PA∩AD=A,
平面OBE∥平面PAD,
∵BE平面PAD,BE平面PAD,
∴BE∥平面PAD
(2)解:∵AC是圆O的一条直径,∴AC⊥AD,
∵PA⊥平面ABCD,∴PA⊥CD,
则CD⊥平面PAD,
则CD⊥PD,
则∠PDA是二面角P﹣CD﹣A的平面角,
若二面角P﹣CD﹣A的正切值为2,
则tan∠PDA= ![]() =2,
=2,
即AD=1,
建立以D为坐标原点,DA,DC,垂直于平面ABCD的直线分别为x,y,z轴的空间直角坐标系如图:
则B( ![]() ,
, ![]() ,0),P(1,0,2),
,0),P(1,0,2), ![]() =(-
=(- ![]() ,﹣
,﹣ ![]() ,2)
,2)
D(0,0,0),C(0, ![]() ,0),
,0),
则 ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(1,0,2),
=(1,0,2),
设平面PCD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 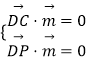 ,即
,即 ![]() ,令z=1,则x=﹣2,y=0,
,令z=1,则x=﹣2,y=0,
即 ![]() =(﹣2,0,1),
=(﹣2,0,1),
则直线PB与平面PCD所成角的正弦值sin< ![]() ,
, ![]() >=|cos<
>=|cos< ![]() ,
, ![]() >|=|
>|=| 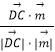 |=
|= ![]()
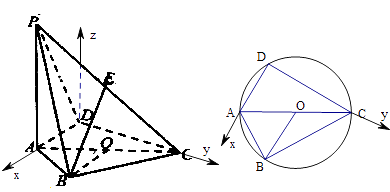
【解析】(1)根据面面平行的性质定理证明平面OBE∥平面PAD,即可证明BE∥平面PAD;(2)建立空间坐标系,根据二面角P﹣CD﹣A的正切值为2,得到AD=1,然后求出平面的法向量,利用直线和平面所成角的定义即可求直线PB与平面PCD所成角的正弦值
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线C:
 ﹣
﹣  =1(a>0,b>0)两条渐近线l1 , l2与抛物线y2=﹣4x的准线1围成区域Ω,对于区域Ω(包含边界),对于区域Ω内任意一点(x,y),若
=1(a>0,b>0)两条渐近线l1 , l2与抛物线y2=﹣4x的准线1围成区域Ω,对于区域Ω(包含边界),对于区域Ω内任意一点(x,y),若  的最大值小于0,则双曲线C的离心率e的取值范围为 .
的最大值小于0,则双曲线C的离心率e的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.

(1)求f(x)的解析式,并求函数f(x)在[﹣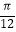 ,
,  ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
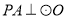 所在的平面,
所在的平面, 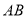 是
是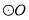 的直径,
的直径, 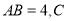 是
是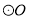 上一点,且
上一点,且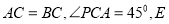 是
是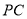 中点,
中点,  为
为 中点.
中点.
(1)求证:
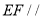 面
面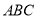 ;
;(2)求证:
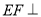 面
面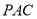 ;
;(3)求三棱锥
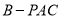 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
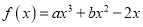 ,且
,且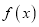 在
在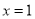 和
和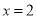 处取得极值.
处取得极值.(Ⅰ)求函数
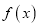 的解析式;
的解析式;(Ⅱ)设函数
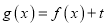 ,是否存在实数
,是否存在实数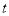 ,使得曲线
,使得曲线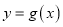 与
与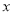 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出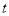 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点
 ,
,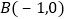 ,圆C的方程为
,圆C的方程为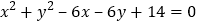 ,点P为圆上的动点.
,点P为圆上的动点.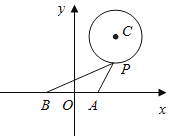
 求过点A的圆C的切线方程.
求过点A的圆C的切线方程. 求
求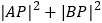 的最大值及此时对应的点P的坐标.
的最大值及此时对应的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ,证明:
,证明:  +
+  +…+
+…+  <
<  Sn+1(n∈N*).
Sn+1(n∈N*).
相关试题

