【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于5.
的距离之比等于5.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为 8,求直线
所截得的线段的长为 8,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() (2)
(2)![]() ,或
,或![]() .
.
【解析】 【试题分析】(1)运用两点间距离公式建立方程进行化简;(2)借助直线与圆的位置关系,运用圆心距、半径、弦长之间的关系建立方程待定直线的斜率,再用直线的点斜式方程分析求解:
(1)由题意,得 ![]()

化简,得![]() .
.
即![]() .
.
![]() 点
点![]() 的轨迹方程是
的轨迹方程是![]()
轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
(2)当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,
,
此时所截得的线段的长为![]() ,
,
![]() 符合题意.
符合题意.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为
![]() ,即
,即![]() ,
,
圆心到![]() 的距离
的距离![]() ,
,
由题意,得 ,
,
解得![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
即![]() .
.
综上,直线![]() 的方程为
的方程为
![]() ,或
,或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心为
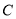 的圆过点
的圆过点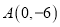 和
和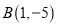 ,且圆心在直线
,且圆心在直线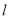 :
: 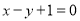 上.
上.(1)求圆心为
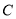 的圆的标准方程;
的圆的标准方程;(2)过点
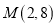 作圆的切线,求切线方程.
作圆的切线,求切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)[(5 )0.5+(0.008)﹣
)0.5+(0.008)﹣  ÷(0.2)﹣1]÷0.06250.25;
÷(0.2)﹣1]÷0.06250.25;
(2)[(1﹣log63)2+log62log618]÷log64. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为[7,15),设f(2x+1)的定义域为A,B={x|x<a或x>a+1},若A∪B=R,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
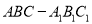 中,
中,  ,顶点
,顶点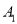 在底面
在底面 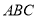 上的射影恰为点
上的射影恰为点 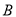 ,且
,且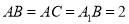 .
.
(1)求棱
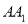 与
与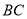 所成的角的大小;
所成的角的大小;(2)在棱
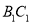 上确定一点
上确定一点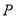 ,使
,使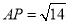 ,并求出二面角
,并求出二面角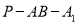 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下说法:①不共面的四点中,任意三点不共线;
②有三个不同公共点的两个平面重合;
③没有公共点的两条直线是异面直线;
④分别和两条异面直线都相交的两条直线异面;
⑤一条直线和两条异面直线都相交,则它们可以确定两个平面.
其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围.
相关试题

