【题目】若圆![]() 上有四个不同的点到直线
上有四个不同的点到直线![]() 的距离为2,则
的距离为2,则![]() 的取值范围是( )
的取值范围是( )
A. (-12,8) B. (-8,12) C. (-13,17) D. (-17,13)
参考答案:
【答案】C
【解析】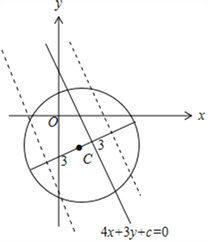 圆C:x2+y2﹣2x+4y﹣20=0化为(x﹣1)2+(y+2)2=25,
圆C:x2+y2﹣2x+4y﹣20=0化为(x﹣1)2+(y+2)2=25,
则圆心C为(1,﹣2),半径r=5.
若圆C:(x﹣1)2+(y+2)2=25有四个不同的点到直线l:4x+3y+c=0的距离为2,
则圆心C(1,﹣2)到直线l的距离d<3, ![]()
即解得:﹣13<c<17,∴c的取值范围是(﹣13,17).
故选:C.
点睛: 由题意画出图形,若圆C:(x﹣1)2+(y+2)2=25有四个不同的点到直线l:4x+3y+c=0的距离为2,则圆心C(1,﹣2)到直线l的距离d<3,由此列关于c的不等式得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过原点的动直线
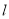 与圆
与圆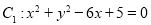 相交于不同的两点
相交于不同的两点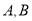 .
.(1)求线段
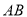 的中点
的中点 的轨迹
的轨迹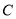 的方程;
的方程;(2)是否存在实数
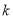 ,使得直线
,使得直线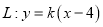 与曲线
与曲线 只有一个交点?若存在,求出
只有一个交点?若存在,求出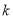 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
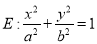 (
(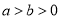 )的离心率为
)的离心率为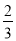 ,
,  分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线 ,使
,使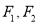 关于
关于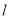 的对称点恰好是圆
的对称点恰好是圆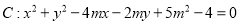 (
(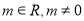 )的一条直线的两个端点.
)的一条直线的两个端点.(1)求椭圆
 的方程;
的方程;(2)设直线
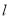 与抛物线
与抛物线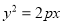 (
(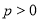 )相交于
)相交于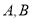 两点,射线
两点,射线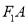 ,
, 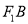 与椭圆
与椭圆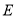 分别相交于点
分别相交于点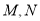 ,试探究:是否存在数集
,试探究:是否存在数集 ,当且仅当
,当且仅当 时,总存在
时,总存在 ,使点
,使点 在以线段
在以线段 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集 ;若不存在,请说明理由.
;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B=

(1)求边c的长;
(2)求角B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 :
: 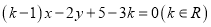 恒过定点
恒过定点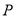 ,圆
,圆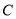 经过点
经过点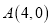 和点
和点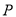 ,且圆心在直线
,且圆心在直线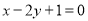 上.
上.(1)求定点
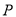 的坐标;
的坐标;(2)求圆
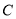 的方程;
的方程;(3)已知点
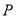 为圆
为圆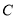 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点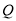 ,问:在
,问:在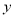 轴上是否存在一点
轴上是否存在一点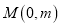 ,使得
,使得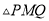 为直角三角形,若存在,求出
为直角三角形,若存在,求出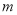 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
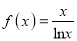 ,
, 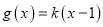 .
.(1)证明:
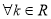 ,直线
,直线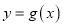 都不是曲线
都不是曲线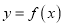 的切线;
的切线;(2)若
 ,使
,使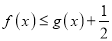 成立,求实数
成立,求实数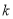 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值
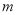
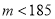
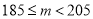
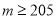
等级
三等品
二等品
一等品
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
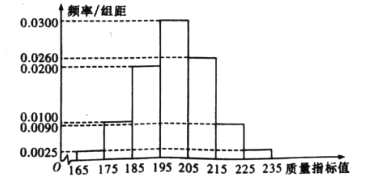
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值
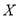 近似满足
近似满足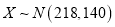 ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
相关试题

