【题目】如图,以![]() 为顶点的六面体中,
为顶点的六面体中, ![]() 和
和![]() 均为等边三角形,且平面
均为等边三角形,且平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
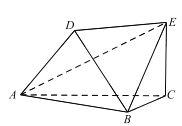
(1)求证: ![]() 平面
平面![]() ;
;
(2)求此六面体的体积.
参考答案:
【答案】(1)证明见解析;(2) 2.
【解析】试题分析:(Ⅰ)作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,根据条件证明四边形
,根据条件证明四边形![]() 是平行四边形;(Ⅱ)将此六面体分成两个三棱锥的体积和
是平行四边形;(Ⅱ)将此六面体分成两个三棱锥的体积和![]() ,根据(Ⅰ)的结果可知点
,根据(Ⅰ)的结果可知点![]() 到平面
到平面![]() 的距离是
的距离是![]() ,点
,点![]() 到平面
到平面![]() 的距离是
的距离是![]() ,这样求体积和.
,这样求体积和.
试题解析:(Ⅰ)作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() .
.
因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
从而![]() .
.
因为![]() 是边长为2的等边三角形,
是边长为2的等边三角形,
所以![]() ,
,
因此![]() ,
,
于是四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
因此![]() 平面
平面![]() .
.
(Ⅱ) 因为![]() 是等边三角形,
是等边三角形,
所以![]() 是
是![]() 中点,
中点,
而![]() 是等边三角形,
是等边三角形,
因此![]() ,
,
由![]() 平面
平面![]() ,知
,知![]() ,
,
从而![]() 平面
平面![]() ,
,
又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因此四面体![]() 的体积为
的体积为![]() ,
,
四面体![]() 的体积为
的体积为![]() ,
,
而六面体![]() 的体积=四面体
的体积=四面体![]() 的体积+四面体
的体积+四面体![]() 的体积
的体积
故所求六面体的体积为2

-
科目: 来源: 题型:
查看答案和解析>>【题目】给定椭圆C:
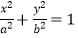 (a>b>0).称圆心在原点O,半径为
(a>b>0).称圆心在原点O,半径为 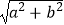 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( 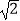 ,0),其短轴上的一个端点到点F的距离为
,0),其短轴上的一个端点到点F的距离为 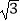 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1 , l2 , 使得l1 , l2与椭圆C都只有一个交点,试判断l1 , l2是否垂直,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过
 的动圆恒与
的动圆恒与 轴相切,设切点为
轴相切,设切点为 是该圆的直径.
是该圆的直径.(Ⅰ)求
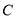 点轨迹
点轨迹 的方程;
的方程;(Ⅱ)当
 不在y轴上时,设直线
不在y轴上时,设直线 与曲线
与曲线 交于另一点
交于另一点 ,该曲线在
,该曲线在 处的切线与直线
处的切线与直线 交于
交于 点.求证:
点.求证:  恒为直角三角形.
恒为直角三角形. -
科目: 来源: 题型:
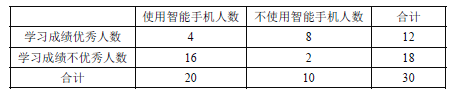
查看答案和解析>>【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
参考数据:

参考公式:
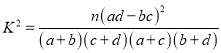 ,其中
,其中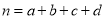
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为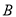 组,计划从
组,计划从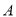 组推选的2人和
组推选的2人和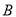 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自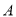 、
、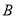 两组的概率.
两组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
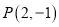 ,求:
,求:(Ⅰ)过
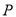 点与原点距离为2的直线
点与原点距离为2的直线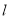 的方程;
的方程;(Ⅱ)过
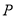 点与原点距离最大的直线
点与原点距离最大的直线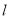 的方程,最大距离是多少?
的方程,最大距离是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗
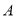 原料1千克、
原料1千克、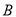 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗 原料2千克,
原料2千克, 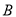 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗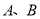 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线:
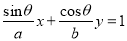 (
(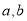 为给定的正常数,
为给定的正常数, 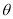 为参数,
为参数, 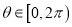 )构成的集合为
)构成的集合为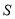 ,给出下列命题:
,给出下列命题:①当
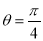 时,
时, 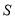 中直线的斜率为
中直线的斜率为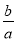 ;
;②
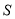 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.③当
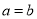 时,存在某个定点,该定点到
时,存在某个定点,该定点到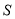 中的所有直线的距离均相等;
中的所有直线的距离均相等;④当
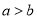 时,
时, 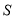 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为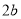 ;
;其中正确的是__________(写出所有正确命题的编号).
相关试题

