【题目】已知函数f(x)=|x﹣3|﹣|x﹣a|.
(1)当a=2时,解不等式f(x)≤﹣ ![]() ;
;
(2)若存在实数x,使得不等式f(x)≥a成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:当a=2时,f(x)=|x﹣3|﹣|x﹣2|,
当x≥3时,f(x)≤﹣ ![]() ,即为(x﹣3)﹣(x﹣2)≤﹣
,即为(x﹣3)﹣(x﹣2)≤﹣ ![]() ,即﹣1
,即﹣1 ![]() 成立,则有x≥3;
成立,则有x≥3;
当x≤2时,f(x)≤﹣ ![]() 即为(3﹣x)﹣(2﹣x)
即为(3﹣x)﹣(2﹣x) ![]() ,即1
,即1 ![]() ,解得x∈;
,解得x∈;
当2<x<3时,f(x)≤﹣ ![]() 即为3﹣x﹣(x﹣2)≤﹣
即为3﹣x﹣(x﹣2)≤﹣ ![]() ,解得,x≥
,解得,x≥ ![]() ,则有
,则有 ![]() ≤x<3.
≤x<3.
则原不等式的解集为[ ![]() ,3)∪[3,+∞)即为[
,3)∪[3,+∞)即为[ ![]() ,+∞)
,+∞)
(2)解:由绝对值不等式的性质可得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,
即有f(x)的最大值为|a﹣3|.
若存在实数x,使得不等式f(x)≥a成立,则有|a﹣3|≥a,
即 ![]() 或
或 ![]() ,即有a∈或a≤
,即有a∈或a≤ ![]() .
.
则a的取值范围是(﹣∞, ![]() ]
]
【解析】(1)运用函数的零点分区间,讨论当x≥3时,当x≤2时,当2<x<3时,化简不等式解得,最后求并集即可;(2)由题意知这是一个存在性的问题,须求出不等式左边的最大值,可运用绝对值不等式的性质可得最大值,再令其大于等于a,即可解出实数a的取值范围.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+
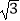 csinB.
csinB.
(1)求B;
(2)若b=2,a=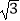 c,求△ABC的面积.
c,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
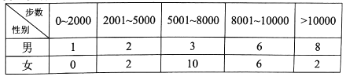
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的
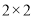 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?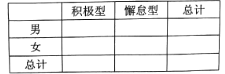
附:
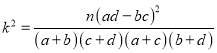 ,
,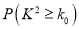
0.10
0.05
0.025
0.010
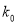
2.706
3.841
5.024
6.635
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有
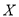 人,超过10000步的有
人,超过10000步的有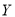 人,设
人,设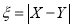 ,求
,求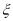 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取
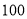 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值 ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.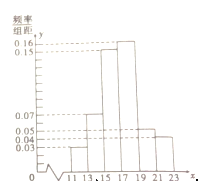
(1)估计该技术指标值
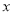 平均数
平均数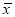 ;
;(2)在直方图的技术指标值分组中,以
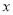 落入各区间的频率作为
落入各区间的频率作为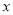 取该区间值的频率,若
取该区间值的频率,若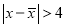 ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取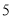 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为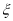 ,求
,求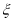 的数学期望
的数学期望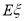 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017四川资阳4月模拟】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
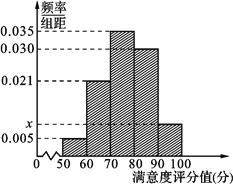
(Ⅰ) 求图中
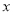 的值;
的值;(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏.

(1)若∠APQ=15°,AP与AQ两处围墙长度和为100(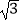 +1)米,求栅栏PQ的长;
+1)米,求栅栏PQ的长;
(2)已知AB,AC的长度均大于200米,若水果园APQ面积为2500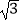 平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
相关试题

