【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
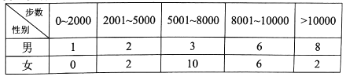
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 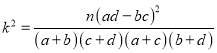 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考答案:
【答案】(Ⅰ)没有95%以上的把握认为二者有关;(Ⅱ)由见解析.
【解析】【试题分析】(1)依据题设条件做成2×2列联表,计算出卡方系数,再与参数进行比对,做出判断;(2)先求随机变量![]() 的分布列,再运用随机变量的数学期望公式计算求解:
的分布列,再运用随机变量的数学期望公式计算求解:
(Ⅰ)
积极型 | 懈怠型 | 总计 | |
男 | 14 | 6 | 20 |
女 | 8 | 12 | 20 |
总计 | 22 | 18 | 40 |
![]() ,故没有95%以上的把握认为二者有关;
,故没有95%以上的把握认为二者有关;
(Ⅱ)由题知,小王的微信好友中任选一人,其每日走路步数不超过5000步的概率为![]() ,超过10000步的概率为
,超过10000步的概率为![]() ,且当
,且当![]() 或
或![]() 时,
时, ![]() ,
, ![]() ;当
;当![]() 或
或
![]() 时,
时, ![]() ,
, ![]() ;当
;当![]() 或
或![]() 时,
时, ![]() ,
,
![]() ,即
,即![]() 的分布列为:
的分布列为:
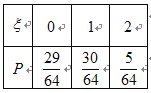
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017广东佛山二模】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为
 、
、 、
、 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).

(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a≠0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为
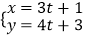 (t为参数).
(t为参数).
(1)求圆C的标准方程和直线l的普通方程;
(2)若直线l与圆C恒有公共点,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+
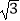 csinB.
csinB.
(1)求B;
(2)若b=2,a=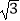 c,求△ABC的面积.
c,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣3|﹣|x﹣a|.
(1)当a=2时,解不等式f(x)≤﹣ ;
;
(2)若存在实数x,使得不等式f(x)≥a成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取
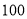 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值 ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.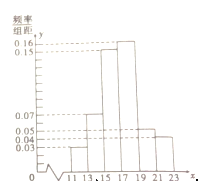
(1)估计该技术指标值
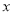 平均数
平均数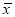 ;
;(2)在直方图的技术指标值分组中,以
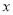 落入各区间的频率作为
落入各区间的频率作为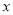 取该区间值的频率,若
取该区间值的频率,若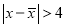 ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取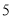 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为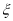 ,求
,求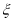 的数学期望
的数学期望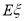 .
.
相关试题

