【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏. 
(1)若∠APQ=15°,AP与AQ两处围墙长度和为100( ![]() +1)米,求栅栏PQ的长;
+1)米,求栅栏PQ的长;
(2)已知AB,AC的长度均大于200米,若水果园APQ面积为2500 ![]() 平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
参考答案:
【答案】
(1)解:∵依题意,∠AQP=45°,由正弦定理: ![]() ,
,
∴得 ![]() ,
,
∵ ![]() ,
,
∴ ![]()
(2)解:设AP=x米,AQ=y米.
则 ![]() xy=10000,
xy=10000,
![]() ,
,
设△ABC的周长为L,则L= ![]() =
= ![]() ,
,
令x+y=t,L= ![]() 在定义域上单调增,
在定义域上单调增,
所以 ![]() ,当x=y=100取等号;
,当x=y=100取等号;
所以当AP=AQ=100米时,三角形地块APQ的周长最小
【解析】(1)依题意,∠AQP=45°,由正弦定理: ![]() ,可得
,可得 ![]() 利用特殊角的三角函数值即可计算得解PQ的值.(2)设AP=x米,AQ=y米,利用三角形面积公式可求xy=10000,进而可求
利用特殊角的三角函数值即可计算得解PQ的值.(2)设AP=x米,AQ=y米,利用三角形面积公式可求xy=10000,进而可求 ![]() ,设△ABC的周长为L,则L=
,设△ABC的周长为L,则L= ![]() =
= ![]() ,令x+y=t,L=
,令x+y=t,L= ![]() 在定义域上单调增,利用二次函数的图象和性质即可得解.
在定义域上单调增,利用二次函数的图象和性质即可得解.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣3|﹣|x﹣a|.
(1)当a=2时,解不等式f(x)≤﹣ ;
;
(2)若存在实数x,使得不等式f(x)≥a成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取
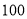 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值 ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.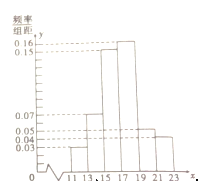
(1)估计该技术指标值
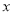 平均数
平均数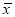 ;
;(2)在直方图的技术指标值分组中,以
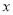 落入各区间的频率作为
落入各区间的频率作为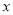 取该区间值的频率,若
取该区间值的频率,若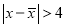 ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取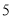 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为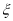 ,求
,求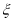 的数学期望
的数学期望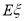 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017四川资阳4月模拟】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
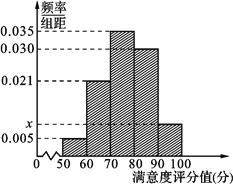
(Ⅰ) 求图中
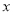 的值;
的值;(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A、B、C所对的边长分别为a,b,c且满足csinA=
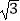 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
A.1
B.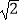
C.3
D.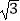
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017山西三区八校二模】已知函数
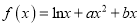 (其中
(其中 ,
, 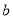 为常数且
为常数且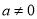 )在
)在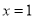 处取得极值.
处取得极值.(Ⅰ)当
 时,求
时,求 的单调区间;
的单调区间;(Ⅱ)若
 在
在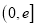 上的最大值为1,求
上的最大值为1,求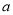 的值.
的值.
相关试题

