【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,若方程
时,若方程![]() 有两个相异实根
有两个相异实根![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
参考答案:
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:(1)对原函数求导![]() ,根据导函数的正负得到函数的单调区间。(2)由条件知
,根据导函数的正负得到函数的单调区间。(2)由条件知![]() 的两个相异实根分别为
的两个相异实根分别为![]() ,构造函数
,构造函数![]() ,研究函数的单调性,得函数递减,由题意可知
,研究函数的单调性,得函数递减,由题意可知![]() ,故
,故![]() ,所以
,所以![]() ,这样就将
,这样就将![]() 化到了同一个单调区间上去,直接研究函数
化到了同一个单调区间上去,直接研究函数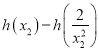 和0的关系即可,最终根据
和0的关系即可,最终根据![]() 的单调性可以得到结果。
的单调性可以得到结果。
解析:(1)因为![]() ,
,
函数![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,当
,当![]() ,即
,即![]() 时,
时, ![]() 对
对![]() 恒成立
恒成立
所以![]() 在
在![]() 上是增函数,
上是增函数,
当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
则![]() 在
在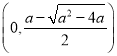 ,
, 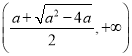 上递增
上递增
在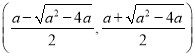 上递减;
上递减;
(2)设![]() 的两个相异实根分别为
的两个相异实根分别为![]() ,满足
,满足![]() ,
,
且![]() ,
, ![]()
令![]() 的导函数
的导函数![]() ,
,
所以![]() 在
在![]() 上递减,由题意可知
上递减,由题意可知![]() ,
,
故![]() ,所以
,所以![]() ,令
,令![]() ,
,
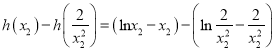
![]()
令![]() ,
,
则![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 是减函数,
是减函数,
所以![]() ,
,
所以当![]() 时,
时, 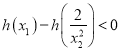 ,
,
因为![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,故
,故![]() ,
,
综上所述, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下四个问题:①x,输出它的绝对值.②求面积为6的正方形的周长.③求三个数a,b,c中最大数.④求函数
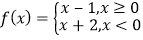 的函数值.其中不需要用条件语句来描述其算法的有 个.
的函数值.其中不需要用条件语句来描述其算法的有 个. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设个人月收入在5000元以内的个人所得税档次为(单位:元):

设某人的月收入为x元,试编一段程序,计算他应交的个人所得税. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
年份
2008
2010
2012
2014
2016
需要量(万件)
236
246
257
276
286
(1)利用所给数据求年需求量y与年份x之间的回归直线方程 =
=  x+
x+  ;
;
(2)预测该地2018年的商品需求量(结果保留整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某种算法的程序,回答下面的问题:
(1)写出输出值y关于输入值x的函数关系式f (x);
(2)当输出的y值小于 时,求输入的x的取值范围.
时,求输入的x的取值范围.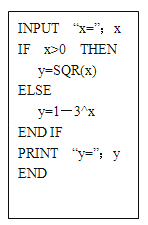
-
科目: 来源: 题型:
查看答案和解析>>【题目】五个数1,2,3,4,a的平均数是3,这五个数的方差是 .
相关试题

