【题目】如图,在正方体![]() 中,
中, ![]() 是
是![]() 的中心,
的中心, ![]() 分别是线段
分别是线段![]() 上的动点,且
上的动点,且![]() ,
, ![]() .
.
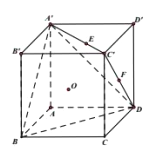
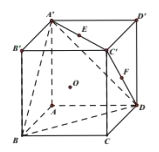
(Ⅰ)若直线![]() 平面
平面![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)若![]() ,正方体
,正方体![]() 的棱长为2,求平面
的棱长为2,求平面![]() 和平面
和平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)取![]() 的中点
的中点![]() ,连
,连![]() ,由直线
,由直线![]() 平面
平面![]() 可证得
可证得![]() ,根据平行线分线段成比例定理可得
,根据平行线分线段成比例定理可得![]() ,即
,即![]() ,得到
,得到![]() ;(Ⅱ)建立空间直角坐标系,求出平面
;(Ⅱ)建立空间直角坐标系,求出平面![]() 的法向量
的法向量![]() 、平面
、平面![]() 的法向量
的法向量![]() ,利用向量的夹角求解即可。
,利用向量的夹角求解即可。
试题解析:
(Ⅰ)取![]() 的中点
的中点![]() ,
,
∵![]() 是正
是正![]() 的中心
的中心
∴点![]() 在
在![]() 上,且
上,且![]() ,
,
连![]() ,
,
∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅱ)当![]() 时,点
时,点![]() 分别是
分别是![]() 的中点,以
的中点,以![]() 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系![]() ,则
,则![]() 。
。
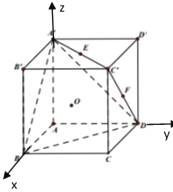
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由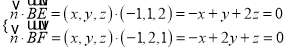 ,
,
得![]() ,令
,令![]() ,得
,得![]() 。
。
同理可得平面![]() 的一个法向量为
的一个法向量为![]()
∴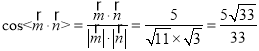 .
.
由图形知,平面![]() 和平面
和平面![]() 所成二面角为锐角,
所成二面角为锐角,
∴平面![]() 和平面
和平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线
(1)若直线
 与圆
与圆 相交于两点
相交于两点 ,弦长
,弦长 等于
等于 ,求
,求 的值;
的值;(2)已知点
 ,点
,点 为圆心,若在直线
为圆心,若在直线 上存在定点
上存在定点 (异于点
(异于点 ),满足:对于圆
),满足:对于圆 上任一点
上任一点 ,都有
,都有 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点 的坐标及改常数.
的坐标及改常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两定点
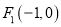 ,
, 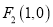 和一动点
和一动点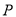 ,给出下列结论:
,给出下列结论:①若
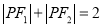 ,则点
,则点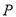 的轨迹是椭圆;
的轨迹是椭圆;②若
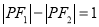 ,则点
,则点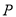 的轨迹是双曲线;
的轨迹是双曲线;③若
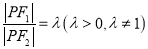 ,则点
,则点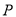 的轨迹是圆;
的轨迹是圆;④若
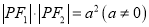 ,则点
,则点 的轨迹关于原点对称;
的轨迹关于原点对称;⑤若直线
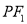 与
与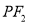 斜率之积等于
斜率之积等于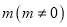 ,则点
,则点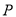 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).其中正确的是__________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 :
: ,
, :
: ,则下面结论正确的是( )
,则下面结论正确的是( )A. 把
 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线
个单位长度,得到曲线
B. 把
 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线
个单位长度,得到曲线
C. 把
 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线
个单位长度,得到曲线
D. 把
 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个 单位长度,得到曲线
单位长度,得到曲线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱
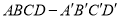 的底面
的底面 是菱形,
是菱形,  ,
, 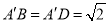 ,
, 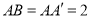 .
.(Ⅰ)证明:平面
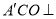 平面
平面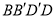 ;
;(Ⅱ)若
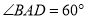 ,直线
,直线 上是否存在点
上是否存在点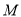 ,使得
,使得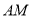 与平面
与平面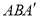 所成角的正弦值为
所成角的正弦值为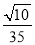 .若存在,求
.若存在,求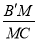 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.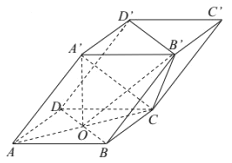
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,圆心为
,圆心为 ,定点
,定点 ,
,  为圆
为圆 上一点,线段
上一点,线段 上一点
上一点 满足
满足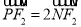 ,直线
,直线 上一点
上一点 ,满足
,满足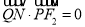 .
.(Ⅰ)求点
 的轨迹
的轨迹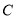 的方程;
的方程;(Ⅱ)
 为坐标原点,
为坐标原点,  是以
是以 为直径的圆,直线
为直径的圆,直线 与
与 相切,并与轨迹
相切,并与轨迹 交于不同的两点
交于不同的两点 .当
.当 且满足
且满足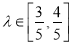 时,求
时,求 面积
面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,随机抽取了
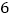 个试销售数据,得到第
个试销售数据,得到第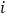 个销售单价
个销售单价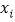 (单位:元)与销售
(单位:元)与销售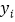 (单位:件)的数据资料,算得
(单位:件)的数据资料,算得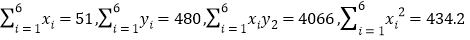
(1)求回归直线方程
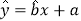 ;
;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是
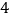 元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)
元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)附:回归直线方程
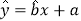 中,
中, ,其中
,其中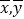 是样本平均值.
是样本平均值.
相关试题

