【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 在
在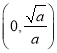 单调递减,在
单调递减,在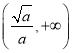 单调递增.
单调递增.
【解析】试题分析:(1)求导数,利用导数的几何意义曲线![]() 在点
在点![]() 处的切线斜率
处的切线斜率![]() 的值,根据点斜式可得切线方程;(2)先求出函数的导数,根据
的值,根据点斜式可得切线方程;(2)先求出函数的导数,根据![]() 解关于
解关于![]() 导函数的不等式可得增区间,
导函数的不等式可得增区间, ![]() 解关于
解关于![]() 的不等式,可求出函数的单调减区间.
的不等式,可求出函数的单调减区间.
试题解析:(1)当![]() 时,函数
时,函数![]() ,
, ![]() ,
,
∴![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)![]() .
.
令![]() ,解得
,解得![]() ;
;
令![]() ,解得
,解得![]() ;
;
∴![]() 在
在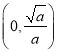 单调递减,在
单调递减,在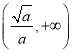 单调递增.
单调递增.
【方法点晴】本题主要考查利用导数求曲线切线以及及利用导数研究函数的单调性,属于中档题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
 及直线外一点
及直线外一点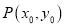 .
.(1)写出点
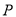 到直线
到直线 的距离公式;
的距离公式;(2)利用向量求证点到直线的距离公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
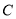 的两个焦点是
的两个焦点是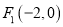 ,
, 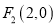 ,且椭圆
,且椭圆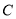 经过点
经过点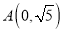 .
.(1)求椭圆
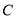 的标准方程;
的标准方程;(2)若过椭圆
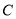 的左焦点
的左焦点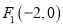 且斜率为1的直线
且斜率为1的直线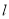 与椭圆
与椭圆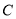 交于
交于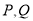 两点,求线段
两点,求线段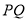 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间(满分100分,成绩不低于40分),现将成绩按如下方式分成6组:第一组
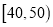 ;第二组
;第二组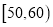 ;……;第六组
;……;第六组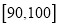 ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间
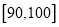 内的概率.
内的概率.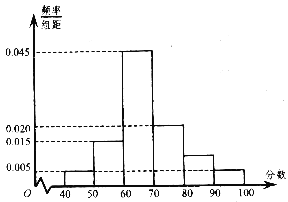
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成
 列联表;
列联表;数学成绩及格
数学成绩不及格
合计
比较细心
45
比较粗心
合计
60
100
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量
 的临界值参考表:
的临界值参考表: 
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 ,其中
,其中
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是
 ,取到方块(事件B)的概率是
,取到方块(事件B)的概率是 ,问:
,问:(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
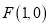 ,点
,点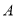 是直线
是直线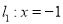 上的动点,过
上的动点,过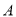 作直线
作直线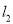 ,
, 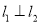 ,线段
,线段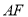 的垂直平分线与
的垂直平分线与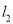 交于点
交于点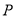 .
.(1)求点
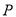 的轨迹
的轨迹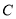 的方程;
的方程;(2)若点
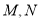 是直线
是直线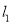 上两个不同的点,且
上两个不同的点,且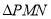 的内切圆方程为
的内切圆方程为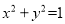 ,直线
,直线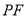 的斜率为
的斜率为 ,求
,求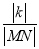 的取值范围.
的取值范围.
相关试题

