【题目】如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是![]() ,取到方块(事件B)的概率是
,取到方块(事件B)的概率是![]() ,问:
,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:
(1)由题意得C=A∪B,由于事件A与事件B互斥,故可由概率加法公式求解。(2)由于事件C与事件D为对立事件,可根据对立事件计算事件D的概率。
试题解析:
(1) 由题意得C=A∪B,且事件A与事件B互斥,
根据概率的加法公式得
P(C)=P(A)+P(B)=![]() 。
。
即取到红色牌(事件C)的概率是![]() 。
。
(2)事件C与事件D互斥,且C∪D为必然事件,因此事件C与事件D是对立事件,
所以P(D)=1-P(C)=![]() 。
。
即取到黑色牌(事件D)的概率是![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间(满分100分,成绩不低于40分),现将成绩按如下方式分成6组:第一组
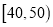 ;第二组
;第二组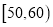 ;……;第六组
;……;第六组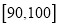 ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间
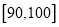 内的概率.
内的概率.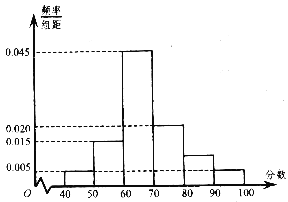
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
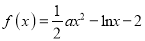 .
.(1)当
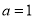 时,求曲线
时,求曲线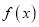 在点
在点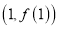 处的切线方程;
处的切线方程;(2)若
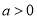 ,求函数
,求函数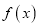 的单调区间.
的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成
 列联表;
列联表;数学成绩及格
数学成绩不及格
合计
比较细心
45
比较粗心
合计
60
100
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量
 的临界值参考表:
的临界值参考表: 
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 ,其中
,其中
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
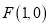 ,点
,点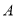 是直线
是直线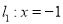 上的动点,过
上的动点,过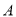 作直线
作直线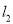 ,
, 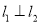 ,线段
,线段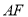 的垂直平分线与
的垂直平分线与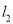 交于点
交于点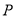 .
.(1)求点
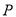 的轨迹
的轨迹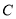 的方程;
的方程;(2)若点
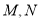 是直线
是直线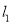 上两个不同的点,且
上两个不同的点,且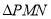 的内切圆方程为
的内切圆方程为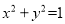 ,直线
,直线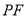 的斜率为
的斜率为 ,求
,求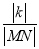 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
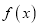 在
在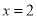 处取得极值,求实数
处取得极值,求实数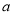 的值;
的值;(2)若函数
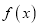 )在区间
)在区间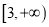 上为增函数,求实数
上为增函数,求实数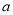 的取值范围;
的取值范围; (3)若当
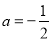 时,方程
时,方程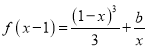 有实数根,求实数
有实数根,求实数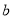 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市英才中学的一个社会实践调查小组,在对中学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对收回的120份有效问卷进行统计,得到如下
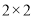 列联表:
列联表:做不到光盘
能做到光盘
合计
男
45
10
55
女
30
15
45
合计
75
25
100
(1)现已按是否能做到光盘分层从45份女生问卷中抽取9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为
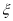 ,试求随机变量
,试求随机变量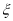 的分布列和数学期望;
的分布列和数学期望;(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过
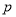 ,那么根据临界值表最精确的
,那么根据临界值表最精确的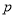 的值应为多少?请说明理由.
的值应为多少?请说明理由.附:独立性检验统计量
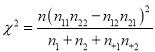 ,其中
,其中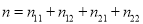 .
.独立性检验临界表:
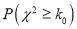
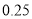

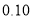
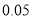
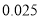
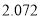
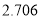
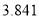
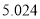
相关试题

