【题目】设直线![]() 及直线外一点
及直线外一点![]() .
.
(1)写出点![]() 到直线
到直线![]() 的距离公式;
的距离公式;
(2)利用向量求证点到直线的距离公式.
参考答案:
【答案】详情见解析
【解析】试题分析:(1)写出平面直角坐标系中,点到直线的距离公式即可;
(2)证明公式时应讨论B=0或A=0以及A≠0,且B≠0时,点到直线l的距离公式是什么,分别求出即可.
试题解析:
(1)平面直角坐标系中,点P(x0,y0)到直线Ax+By+C=0的距离为
![]() ;
;
(2)证明:设PQ垂直直线l于Q,
当B=0时,直线l为:x=CA,所以![]() ,满足公式;
,满足公式;
当A=0时,直线l为:y=CB,所以![]() ,满足公式;
,满足公式;
当A≠0,且B≠0时,直线l与x轴、y轴都相交,
过点P作x轴的平行线,交l与点R(x1,y0),作y轴的平行线交l于点S(x0,y2),
如图所示: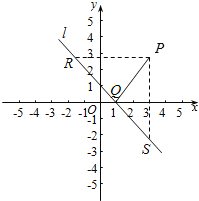
把点R的坐标代入l的方程,求出x1=By0+CA,
把点S的坐标代入l的方程,求出y2=Ax0+CB,
所以|PR|=|x0x1|=|Ax0+By0+CA|,
|PS|=|y0y2|=|Ax0+By0+CB|,
|RS|= ![]() ;
;
由三角形的面积公式,得d|RS|=|PR||PS|,
所以d=|PQ|= ![]() ;
;
综上,点P(x0,y0)到直线Ax+By+C=0的距离为
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线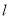 过点
过点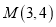 ,其倾斜角为
,其倾斜角为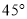 ,以原点为极点,以
,以原点为极点,以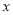 正半轴为极轴建立极坐标,并使得它与直角坐标系
正半轴为极轴建立极坐标,并使得它与直角坐标系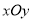 有相同的长度单位,圆
有相同的长度单位,圆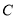 的极坐标方程为
的极坐标方程为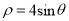 .
.(1)求直线
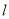 的参数方程和圆
的参数方程和圆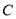 的普通方程;
的普通方程;(2)设圆
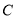 与直线
与直线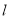 交于点
交于点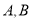 ,求
,求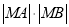 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.(1)已知二次函数
 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;(2)若
 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;(3)若
 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的月固定成本为10(万元),每生产
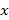 件,需另投入成本为
件,需另投入成本为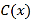 (万元).当月产量不足30件时,
(万元).当月产量不足30件时, 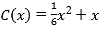 (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, 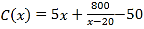 (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.(1)写出月利润
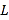 (万元)关于月产量
(万元)关于月产量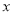 (件)的函数解析式;
(件)的函数解析式;(2)当月产量为多少件时,该厂所获月利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
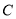 的两个焦点是
的两个焦点是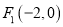 ,
, 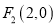 ,且椭圆
,且椭圆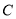 经过点
经过点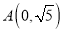 .
.(1)求椭圆
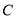 的标准方程;
的标准方程;(2)若过椭圆
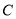 的左焦点
的左焦点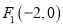 且斜率为1的直线
且斜率为1的直线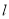 与椭圆
与椭圆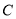 交于
交于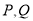 两点,求线段
两点,求线段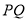 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间(满分100分,成绩不低于40分),现将成绩按如下方式分成6组:第一组
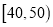 ;第二组
;第二组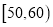 ;……;第六组
;……;第六组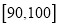 ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间
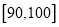 内的概率.
内的概率.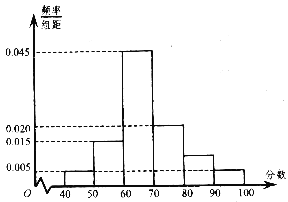
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
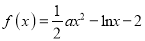 .
.(1)当
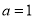 时,求曲线
时,求曲线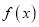 在点
在点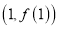 处的切线方程;
处的切线方程;(2)若
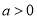 ,求函数
,求函数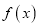 的单调区间.
的单调区间.
相关试题

