【题目】在直角坐标系中,曲线C的参数方程: ![]() ,直线l的参数方程为
,直线l的参数方程为 ![]() .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若 ![]() ,求实数a.
,求实数a.
参考答案:
【答案】
(1)解:∵曲线C的参数方程: 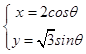 ,
,
∴曲线C的普通方程为 ![]() =1,
=1,
∵直线l的参数方程为 ![]() ,
,
∴直线l的普通方程为x+2y﹣a﹣2=0,
联立 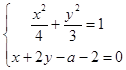 ,得16y2﹣(12a+24)y+3a2+12a=0,
,得16y2﹣(12a+24)y+3a2+12a=0,
∵直线l与曲线C只有一个公共点,
∴△=[﹣(12a+24)]2﹣4×16×(3a2+12a)=﹣a2﹣4a+12=0,
解得a=2或a=﹣6
(2)解:设Q(2cosθ, ![]() ),
),
点Q到直线l的距离d= 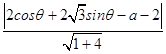 =
= ![]() |4sin(
|4sin( ![]() )﹣a﹣2|,
)﹣a﹣2|,
∵点P,Q分别为直线l与曲线C上的动点, ![]() ,
,
∴当sin( ![]() )=1时,|PQ|min=
)=1时,|PQ|min= ![]() |2﹣a|=
|2﹣a|= ![]() ,
,
解得a=1或a=3
【解析】(1)由曲线C的参数方程求出曲线C的普通方程为 ![]() =1,由直线l的参数方程求出直线l的普通方程为x+2y﹣a﹣2=0,联立
=1,由直线l的参数方程求出直线l的普通方程为x+2y﹣a﹣2=0,联立 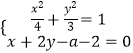 ,得16y2﹣(12a+24)y+3a2+12a=0,由直线l与曲线C只有一个公共点,利用根的判别式为0,能求出a.(2)设Q(2cosθ,
,得16y2﹣(12a+24)y+3a2+12a=0,由直线l与曲线C只有一个公共点,利用根的判别式为0,能求出a.(2)设Q(2cosθ, ![]() ),求出点Q到直线l的距离d=
),求出点Q到直线l的距离d= ![]() |4sin(
|4sin( ![]() )﹣a﹣2|,由题意知当sin(
)﹣a﹣2|,由题意知当sin( ![]() )=1时,|PQ|min=
)=1时,|PQ|min= ![]() |2﹣a|=
|2﹣a|= ![]() ,由此能求出a.
,由此能求出a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐园的摩天轮最高点距离地面108米,直径长是98米,均速旋转一圈需要18分钟.如果某人从摩天轮的最低点
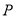 处登上摩天轮并开始计时,那么:
处登上摩天轮并开始计时,那么:
(1)当此人第四次距离地面
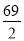 米时用了多少分钟?
米时用了多少分钟?(2)当此人距离地面不低于
 米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若
 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;(2)若函数
 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;(3)若存在实数
 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x+a|.
(1)若a=2,解关于x的不等式f(x)+f(x﹣3)≥5;
(2)若关于x的不等式f(x)﹣f(x+2)+4≥|1﹣3m|恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值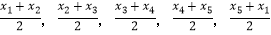 的概率均为
的概率均为 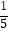 ,随机变量Y取值
,随机变量Y取值 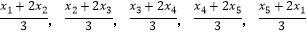 的概率也均为
的概率也均为 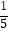 ,比较DX与DY大小关系.
,比较DX与DY大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】近来景德镇市棚户区改造进行的如火如荼,加上城市人居环境的不断改善,我市房地产住宅销售价格节节攀升,一部分刚需住户带来了不小的烦恼,下表为我市2017.1﹣2017.5这5月住宅价格与月份的关系.
月份x
1
2
3
4
5
住宅价格y
千元/平米4.8
5.4
6.2
6.6
7
(1)通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度(精确到0.01)
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系. ①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(m-1,2),B(1,1),C(3,m2-m-1).
(1)若A,B,C三点共线,求实数m的值;
(2)若AB⊥BC,求实数m的值.
相关试题

