【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() 使得关于
使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)奇函数,(2)![]() ,(3)
,(3) ![]()
【解析】
试题分析:(1)函数奇偶性的判定,一要判定定义域是否关于原点对称,二要判定![]() 与
与![]() 是否相等或相反,(2)函数
是否相等或相反,(2)函数![]() 是分段函数,每一段都是二次函数的一部分,因此研究
是分段函数,每一段都是二次函数的一部分,因此研究![]() 单调性,必须研究它们的对称轴,从图像可观察得到实数
单调性,必须研究它们的对称轴,从图像可观察得到实数![]() 满足的条件:
满足的条件:![]() ,(3)研究方程根的个数,通常从图像上研究,结合(2)可研究出函数
,(3)研究方程根的个数,通常从图像上研究,结合(2)可研究出函数![]() 图像.分三种情况研究,一是
图像.分三种情况研究,一是![]() 上单调增函数,二是先在
上单调增函数,二是先在![]() 上单调增,后在
上单调增,后在![]() 上单调减,再在
上单调减,再在![]() 上单调增,三是先在
上单调增,三是先在![]() 上单调增,后在
上单调增,后在![]() 上单调减,再在
上单调减,再在![]() 上单调增.
上单调增.
试题解析:(1)函数![]() 为奇函数.[来
为奇函数.[来
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]()
∴函数![]() 为奇函数; 3分
为奇函数; 3分
(2)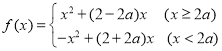 ,当
,当![]() 时,
时,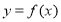 的对称轴为:
的对称轴为:![]() ;
;
当![]() 时,
时,![]() 的对称轴为:
的对称轴为:![]() ;∴当
;∴当![]() 时,
时,![]() 在R上是增函数,即
在R上是增函数,即![]() 时,函数
时,函数![]() 在
在![]() 上是增函数; 7分
上是增函数; 7分
(3)方程![]() 的解即为方程
的解即为方程![]() 的解.
的解.
①当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数,∴关于
上是增函数,∴关于![]() 的方程
的方程![]() 不可能有三个不相等的实数根; 9分
不可能有三个不相等的实数根; 9分
②当![]() 时,即
时,即![]() ,∴
,∴![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,在
上单调减,在![]() 上单调增,∴当
上单调增,∴当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有三个不相等的实数根;即
有三个不相等的实数根;即,∵
![]() ∴
∴![]() .
.
设![]() ,∵存在
,∵存在![]() 使得关于
使得关于![]() 的方程
的方程![]() 有三个不相等的实数根, ∴
有三个不相等的实数根, ∴![]() ,又可证
,又可证![]() 在
在![]() 上单调增
上单调增
∴![]() ∴
∴![]() ; 12分
; 12分
③当![]() 时,即
时,即![]() ,∴
,∴![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,在
上单调减,在![]() 上单调增,
上单调增,
∴当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有三个不相等的实数根;
有三个不相等的实数根;
即![]() ,∵
,∵![]() ∴
∴![]() ,设
,设![]()
∵存在![]() 使得关于
使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,
有三个不相等的实数根,
∴![]() ,又可证
,又可证![]() 在
在![]() 上单调减∴
上单调减∴![]()
∴![]() ; 15分
; 15分
综上:![]() . 16分
. 16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,当
,当 时,恒有
时,恒有 .当
.当 时,
时,  .
.(Ⅰ)求证:
 是奇函数;
是奇函数;(Ⅱ)若
 ,试求
,试求 在区间
在区间 上的最值;
上的最值;(Ⅲ)是否存在
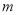 ,使
,使 对于任意
对于任意 恒成立?若存在,求出实数
恒成立?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C极坐标方程:
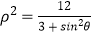 ,点P极坐标为
,点P极坐标为 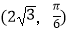 ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为  .
.
(1)求曲线C的直角坐标方程及直线l参数方程;
(2)若直线l与曲线C交于A,B两点,求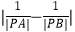 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐园的摩天轮最高点距离地面108米,直径长是98米,均速旋转一圈需要18分钟.如果某人从摩天轮的最低点
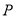 处登上摩天轮并开始计时,那么:
处登上摩天轮并开始计时,那么: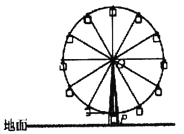
(1)当此人第四次距离地面
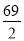 米时用了多少分钟?
米时用了多少分钟?(2)当此人距离地面不低于
 米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x+a|.
(1)若a=2,解关于x的不等式f(x)+f(x﹣3)≥5;
(2)若关于x的不等式f(x)﹣f(x+2)+4≥|1﹣3m|恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,曲线C的参数方程:
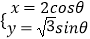 ,直线l的参数方程为
,直线l的参数方程为 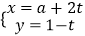 .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若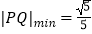 ,求实数a.
,求实数a. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值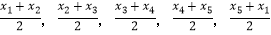 的概率均为
的概率均为 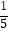 ,随机变量Y取值
,随机变量Y取值 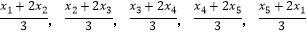 的概率也均为
的概率也均为 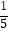 ,比较DX与DY大小关系.
,比较DX与DY大小关系.
相关试题

