【题目】已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0,且直线l与圆C交于A、B两点.
(1)若|AB|= ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P(1,1),满足2 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
参考答案:
【答案】
(1)解:由于半径r= ![]() ,|AB|=
,|AB|= ![]() ,∴弦心距d=
,∴弦心距d= ![]() ,
,
再由点到直线的距离公式可得d= ![]() =
= ![]() ,
,
解得m=± ![]() .
.
故直线的斜率等于± ![]() ,故直线的倾斜角等于
,故直线的倾斜角等于 ![]() 或
或 ![]()
(2)解:设点A(x1,mx1﹣m+1),点B(x2,mx2﹣m+1 ),
由题意2 ![]() =
= ![]() ,可得 2(1﹣x1,﹣mx1+m )=(x2﹣1,mx2﹣m ),
,可得 2(1﹣x1,﹣mx1+m )=(x2﹣1,mx2﹣m ),
∴2﹣2x1=x2﹣1,即2x1+x2=3. ①
再把直线方程 y﹣1=m(x﹣1)代入圆C:x2+(y﹣1)2=5,化简可得 (1+m2)x2﹣2m2x+m2﹣5=0,
由根与系数的关系可得x1+x2= ![]() ②.
②.
由①②解得x1= ![]() ,故点A的坐标为(
,故点A的坐标为( ![]() ,
, ![]() ).
).
把点A的坐标代入圆C的方程可得m2=1,故m=±1,
故直线L的方程为x﹣y=0,或x+y﹣2=0.
【解析】(1)求出弦心距、利用点到直线的距离公式可得直线的斜率,即可求直线l的倾斜角;(2)设点A(x1 , mx1﹣m+1),点B(x2 , mx2﹣m+1 ),由题意2 ![]() =
= ![]() ,可得2x1+x2=3. ①再把直线方程 y﹣1=m(x﹣1)代入圆C,化简可得x1+x2=
,可得2x1+x2=3. ①再把直线方程 y﹣1=m(x﹣1)代入圆C,化简可得x1+x2= ![]() ②,由①②解得点A的坐标,把点A的坐标代入圆C的方程求得m的值,从而求得直线L的方程.
②,由①②解得点A的坐标,把点A的坐标代入圆C的方程求得m的值,从而求得直线L的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个古典型(或几何概型)中,若两个不同随机事件
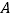 、
、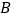 概率相等,则称
概率相等,则称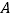 和
和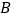 是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.
是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.①在同一个古典概型中,所有的基本事件之间都是“等概率事件”;
②若一个古典概型的事件总数为大于2的质数,则在这个古典概型中除基本事件外没有其他“等概率事件”;③因为所有必然事件的概率都是1,所以任意两个必然事件是“等概率事件”;
④随机同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=-
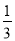 x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sin(2x﹣
 ),x∈R.
),x∈R. 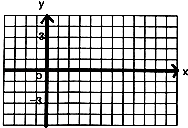
(1)在给定的平面直角坐标系中,画函数f(x)=2sin(2x﹣ ),x∈[0,π]的简图;
),x∈[0,π]的简图;
(2)求f(x)=2sin(2x﹣ ),x∈[﹣π,0]的单调增区间;
),x∈[﹣π,0]的单调增区间;
(3)函数g(x)=2cos2x的图象只经过怎样的平移变换就可得到f(x)=2sin(2x﹣ ),x∈R的图象?
),x∈R的图象? -
科目: 来源: 题型:
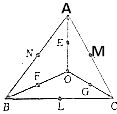
查看答案和解析>>【题目】平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设
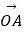 =
= 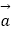 ,
, 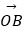 =
= 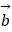 ,
, 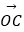 =
= 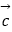 .
. 
(1)试用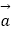 ,
, 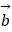 ,
, 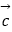 表示向量
表示向量 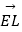 ,
, 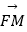 ,
, 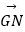 ;
;
(2)证明:线段EL,FM,GN交于一点且互相平分. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点C(t,
 )(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
)(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)当t=2时,求圆C的方程;
(2)求证:△OAB的面积为定值;
(3)设直线y=﹣2x+4与圆C交于点M,N,若|OM|=|ON|,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 的离心率为
的离心率为 ,圆心在
,圆心在 轴的正半轴上的圆
轴的正半轴上的圆 与双曲线的渐近线相切,且圆
与双曲线的渐近线相切,且圆 的半径为2,则以圆
的半径为2,则以圆 的圆心为焦点的抛物线的标准方程为( )
的圆心为焦点的抛物线的标准方程为( )A.
 B.
B. 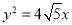 C.
C.  D.
D. 
相关试题

