【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若点![]() 的横坐标为1,求
的横坐标为1,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
参考答案:
【答案】见解析
【解析】(Ⅰ)由椭圆的离心率![]() ,可得
,可得![]() .
.
所以![]() ,所以
,所以![]() .
.
又因为点![]() 在椭圆上,
在椭圆上,
所以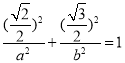 ,即
,即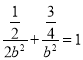 .
.
解得![]() ,故
,故![]() .
.
∴椭圆![]() 的方程为
的方程为![]() . -----------------4分
. -----------------4分
(Ⅱ)椭圆的左焦点为![]() .
.
(ⅰ)当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
直线![]() 的斜率
的斜率 ,所以
,所以![]() .
.
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
而![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离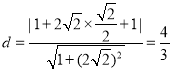 .
.
所以![]() 面积
面积![]() . ----------------- 8分
. ----------------- 8分
(ⅱ)设直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() .
.
联立方程组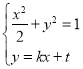 ,
,
消![]() 得,
得,![]() -----------------10分
-----------------10分
由根与系数的关系可得![]() ,
,![]() .
.
所以![]()
![]()
![]()
所以![]()
即![]()
代入整理,![]()
整理得![]() . -----------------13分
. -----------------13分
所以直线![]() 的方程为
的方程为![]() ,
,
所以直线![]() 总过定点
总过定点![]() . -----------------14分
. -----------------14分
【命题意图】本题考查椭圆的方程与性质、直线和椭圆的位置关系、三角形面积的求解以及定点的探究性问题,意在考查基本的逻辑推理能力、运算能力和数学应用意识等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
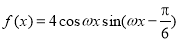 (
(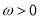 )的对称中心到对称轴距离的最小值为
)的对称中心到对称轴距离的最小值为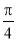 .
.(Ⅰ)求
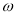 ;
;(Ⅱ)
 中,角
中,角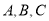 的对边分别为
的对边分别为 .已知锐角
.已知锐角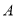 为函数
为函数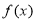 的一个零点,且
的一个零点,且 ,
,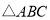 的面积
的面积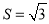 ,求
,求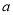 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在[﹣2,2]上的奇函数f(x)=x5+x3+b
(1)求b值;
(2)若f(x)在[0,2]上单调递增,且f(m)+f(m﹣1)>0,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数f(x)是R上的增函数,已知f[f(x)]=16x+5,g(x)=f(x)(x+m).
(1)求f(x);
(2)若g(x)在(1,+∞)单调递增,求实数m的取值范围;
(3)当x∈[﹣1,3]时,g(x)有最大值13,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(2cos
=(2cos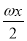 ,
,  sin
sin ),
), =(cos
=(cos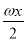 ,2cos
,2cos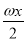 ),(ω>0),设函数f(x)=
),(ω>0),设函数f(x)=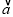
 ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.(1)求函数f(x)的表达式;
(2)求f(x)的单调递增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.y=x+1与y=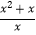
B.f(x)=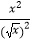 与g(x)=x
与g(x)=x
C.f(x)=|x|与g(x)=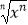
D.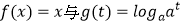
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知椭圆
 过点A(2,1),离心率为
过点A(2,1),离心率为 .
.(Ⅰ)求椭圆的方程;
(Ⅱ)若直线
 与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且
与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且 ,求直线l的方程.
,求直线l的方程.
相关试题

