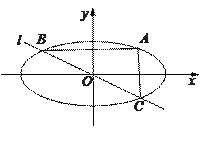
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 过点A(2,1),离心率为
过点A(2,1),离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() 与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且
与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且![]() ,求直线l的方程.
,求直线l的方程.

参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由离心率知![]() ,椭圆过点A(2,1),代入椭圆方程
,椭圆过点A(2,1),代入椭圆方程![]() ,可解得
,可解得![]() .(2)由题意可得直线BC一定过(0,0)点,即m=0, 设
.(2)由题意可得直线BC一定过(0,0)点,即m=0, 设![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,又
,又![]() ,即
,即![]() 代入坐标运算可解得k.
代入坐标运算可解得k.
试题解析:(Ⅰ)由条件知椭圆![]() 离心率为
离心率为 ![]() ,
,
所以![]() .
.
又点A(2,1)在椭圆![]() 上,
上,
所以![]() , 解得
, 解得![]()
所以,所求椭圆的方程为![]() .
.
(Ⅱ)将![]() 代入椭圆方程,得
代入椭圆方程,得![]() ,
,
整理,得![]() . ①
. ①
由线段BC被y轴平分,得![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为当![]() 时,
时, ![]() 关于原点对称,设
关于原点对称,设![]() ,
,
由方程①,得![]() ,
,
又因为![]() ,A(2,1),
,A(2,1),
所以![]()
![]() ,
,
所以![]() .
.
由于![]() 时,直线
时,直线![]() 过点A(2,1),故
过点A(2,1),故![]() 不符合题设.
不符合题设.
所以,此时直线l的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 的离心率为
的离心率为 ,且过点
,且过点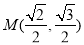 .
.
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)已知椭圆的左焦点为
 ,直线
,直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,
,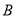 (
( 都在
都在 轴上方),且
轴上方),且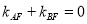 .
.(ⅰ)若点
 的横坐标为1,求
的横坐标为1,求 的面积;
的面积;(ⅱ)直线
 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(2cos
=(2cos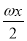 ,
,  sin
sin ),
), =(cos
=(cos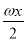 ,2cos
,2cos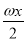 ),(ω>0),设函数f(x)=
),(ω>0),设函数f(x)=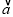
 ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.(1)求函数f(x)的表达式;
(2)求f(x)的单调递增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.y=x+1与y=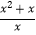
B.f(x)=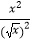 与g(x)=x
与g(x)=x
C.f(x)=|x|与g(x)=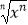
D.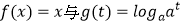
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
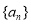 的前
的前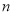 项和为
项和为 ,
,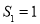 ,
,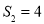 ,且当
,且当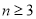 时,
时, 是
是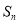 与
与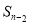 的等差中项.数列
的等差中项.数列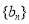 为等比数列,且
为等比数列,且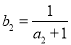 ,
,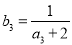 .
.(Ⅰ)求数列
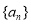 、
、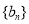 的通项公式;
的通项公式;(Ⅱ)求数列
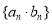 的前
的前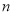 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】五边形
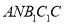 是由一个梯形
是由一个梯形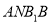 与一个矩形
与一个矩形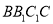 组成的,如图甲所示,B为AC的中点,
组成的,如图甲所示,B为AC的中点, 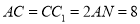 . 先沿着虚线
. 先沿着虚线 将五边形
将五边形 折成直二面角
折成直二面角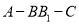 ,如图乙所示.
,如图乙所示.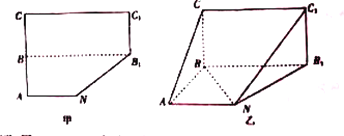
(Ⅰ)求证:平面
 平面
平面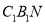 ;
;(Ⅱ)求图乙中的多面体的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)的定义域为[﹣1,5],则函数y=f(3x﹣5)的定义域为( )
A.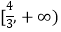
B.[ ,
, 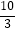 ]
]
C.[﹣8,10]
D.(CRA)∩B
相关试题

