【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.
(Ⅰ)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
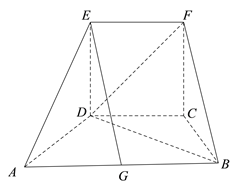
参考答案:
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】试题分析: (1)由![]() //
// ![]() ,且
,且![]() ,故四边形
,故四边形![]() 为平行四边形,所以
为平行四边形,所以![]() //
// ![]() .所以
.所以![]() //平面
//平面![]() ; (2)因为平面
; (2)因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . 在△
. 在△![]() 中,由余弦定理,得
中,由余弦定理,得![]() ,所以
,所以![]() , 如图,以
, 如图,以![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间坐标系,写出各点坐标,求出平面的法向量,根据线面角公式求值即可; (3)假设线段
轴,建立空间坐标系,写出各点坐标,求出平面的法向量,根据线面角公式求值即可; (3)假设线段![]() 上存在点
上存在点![]() ,设
,设 ,分别求出两个平面的法向量,令数量积为0,方程无解,故不存在.
,分别求出两个平面的法向量,令数量积为0,方程无解,故不存在.
试题解析:(Ⅰ)证明:由已知得![]() //
// ![]() ,且
,且![]() .
.
因为![]() 为等腰梯形,所以有
为等腰梯形,所以有![]() //
// ![]() .
.
因为![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() .
.
所以![]() //
// ![]() ,且
,且![]() ,
,
故四边形![]() 为平行四边形,
为平行四边形,
所以![]() //
// ![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
解: (Ⅱ)因为四边形
(Ⅱ)因为四边形![]() 为正方形,所以
为正方形,所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
在△![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以由余弦定理,得![]() ,
,
所以![]() .
.
在等腰梯形![]() 中,可得
中,可得![]() .
.
如图,以![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,
建立空间坐标系,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,  ,
,
所以![]() ,
,  ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由
所以 ,取
,取![]() ,则
,则![]() ,得
,得![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则 ,
,
![]()
所以![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
(Ⅲ)线段![]() 上不存在点
上不存在点![]() ,使平面
,使平面![]()
![]() 平面
平面![]() .证明如下:
.证明如下:
假设线段![]() 上存在点
上存在点![]() ,设
,设 ,
,
则 .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由
所以 ,
,
取![]() ,则
,则![]() ,得
,得![]() .
.
要使平面 平面
平面![]() ,只需
,只需![]() ,
,
即![]() , 此方程无解.
, 此方程无解.
所以线段![]() 上不存在点
上不存在点![]() ,使平面
,使平面![]()
![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
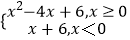 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )
A.(﹣3,1)∪(3,+∞)
B.(﹣3,1)∪(2,+∞)
C.(﹣1,1)∪(3,+∞)
D.(﹣∞,﹣3)∪(1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在圆
在圆 上,
上,  的坐标分别为
的坐标分别为 ,
,  ,线段
,线段 的垂直平分线交线段
的垂直平分线交线段 于点
于点
(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)设圆
 与点
与点 的轨迹
的轨迹 交于不同的四个点
交于不同的四个点 ,求四边形
,求四边形 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度. 药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
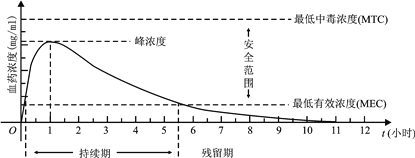
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的个数是
①首次服用该药物1单位约10分钟后,药物发挥治疗作用
②每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
③每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
④首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市购进了A,B,C,D四种新产品,为了解新产品的销售情况,该超市随机调查了15位顾客(记为
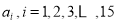 )购买这四种新产品的情况,记录如下(单位:件):
)购买这四种新产品的情况,记录如下(单位:件):顾
客
产
品
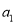
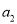
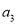
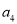
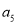
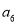
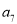
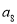
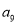
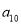

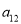

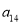
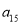
A
1
1
1
1
1
B
1
1
1
1
1
1
1
1
C
1
1
1
1
1
1
1
D
1
1
1
1
1
1
(Ⅰ)若该超市每天的客流量约为300人次,一个月按30天计算,试估计产品A的月销售量(单位:件);
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,
求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解消费者购物情况,某购物中心在电脑小票中随机抽取
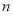 张进行统计,将结果分成6组,分别是:
张进行统计,将结果分成6组,分别是: 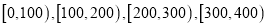 ,
, 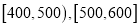 ,制成如下所示的频率分布直方图(假设消费金额均在
,制成如下所示的频率分布直方图(假设消费金额均在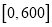 元的区间内).
元的区间内).(1)若在消费金额为
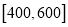 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自
元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自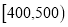 元和
元和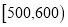 元区间(两区间都有)的概率;
元区间(两区间都有)的概率;(2)为做好春节期间的商场促销活动,商场设计了两种不同的促销方案.

方案一:全场商品打八五折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合P={y|y=(
 )x , x>0},Q={x|y=lg(2x﹣x2)},则(RP)∩Q为( )
)x , x>0},Q={x|y=lg(2x﹣x2)},则(RP)∩Q为( )
A.[1,2)
B.(1,+∞)
C.[2,+∞)
D.[1,+∞)
相关试题

