【题目】设函数f(x)= ![]() 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )
A.(﹣3,1)∪(3,+∞)
B.(﹣3,1)∪(2,+∞)
C.(﹣1,1)∪(3,+∞)
D.(﹣∞,﹣3)∪(1,3)
参考答案:
【答案】A
【解析】解:f(1)=3,当不等式f(x)>f(1)即:f(x)>3
如果x<0 则 x+6>3可得 x>﹣3,可得﹣3<x<0.
如果 x≥0 有x2﹣4x+6>3可得x>3或 0≤x<1
综上不等式的解集:(﹣3,1)∪(3,+∞)
故选A.
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=log
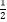
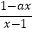 为奇函数,a为常数,
为奇函数,a为常数,
(1)求a的值;
(2)证明f(x)在区间(1,+∞)上单调递增;
(3)若x∈[3,4],不等式f(x)>( )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )

A.14
B.10
C.7
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log
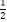 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在圆
在圆 上,
上,  的坐标分别为
的坐标分别为 ,
,  ,线段
,线段 的垂直平分线交线段
的垂直平分线交线段 于点
于点
(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)设圆
 与点
与点 的轨迹
的轨迹 交于不同的四个点
交于不同的四个点 ,求四边形
,求四边形 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度. 药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
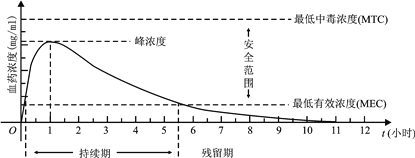
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的个数是
①首次服用该药物1单位约10分钟后,药物发挥治疗作用
②每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
③每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
④首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体中,四边形
 为等腰梯形,
为等腰梯形, 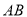 ∥
∥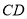 ,
, 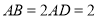 ,
, 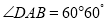 ,四边形
,四边形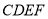 为正方形,平面
为正方形,平面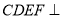 平面
平面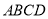 .
.(Ⅰ)若点
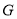 是棱
是棱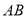 的中点,求证:
的中点,求证: 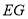 ∥平面
∥平面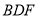 ;
;(Ⅱ)求直线
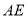 与平面
与平面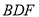 所成角的正弦值;
所成角的正弦值;(Ⅲ)在线段
 上是否存在点
上是否存在点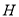 ,使平面
,使平面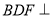 平面
平面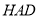 ?若存在,求
?若存在,求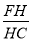 的值;若不存在,说明理由.
的值;若不存在,说明理由.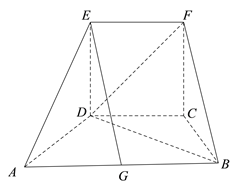
相关试题

