【题目】已知函数f(x)=ax+ ![]() 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ![]() ,1]上的值域.
,1]上的值域.
参考答案:
【答案】
(1)解:∵f(x)的图象过A(1,1)、B(2,﹣1),
∴ 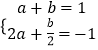 ,解得
,解得 ![]() ,
,
∴ ![]()
(2)证明:设任意x1,x2∈(0,+∞),且x1<x2,
f(x1)﹣f(x2)=(﹣x1+ ![]() )﹣(﹣x2+
)﹣(﹣x2+ ![]() )
)
=(x2﹣x1)+ ![]() =
= ![]()
由x1,x2∈(0,+∞)得,x1x2>0,x1x2+2>0.
由x1<x2得,x2﹣x1>0,
∴f(x1)﹣f(x2)>0,即f(x1)>f(x2),
∴函数 ![]() 在(0,+∞)上为减函数
在(0,+∞)上为减函数
(3)解:由(2)知,函数 ![]() 在[
在[ ![]() ,1]上为减函数,
,1]上为减函数,
∴f(x)min=f(1)=1, ![]() ,
,
∴f(x)的值域是 ![]()
【解析】(1)将点A、B的坐标代入解析式列出方程,求出a、b的值,即可求出f(x);(2)利用定义法证明函数单调性步骤:取值、作差、变形、定号、下结论进行证明;(3)由(2)判断f(x)在[ ![]() ,1]上的单调性,由单调性求出最值,即可得到f(x)的值域.
,1]上的单调性,由单调性求出最值,即可得到f(x)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
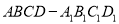 中,侧面
中,侧面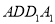 和侧面
和侧面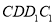 都是矩形,
都是矩形, 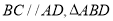 是边长为
是边长为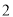 的正三角形,
的正三角形, 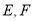 分别为
分别为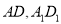 的中点.
的中点.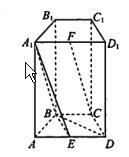
(1)求证:
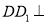 平面
平面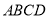 ;
;(2)求证:平面
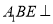 平面
平面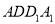 .
.(3)若
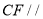 平面
平面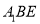 ,求棱
,求棱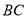 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=5
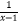 +
+ 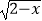 的定义域为( )
的定义域为( )
A.{x|1<x≤2}
B.{x|1≤x≤2}
C.{x|x≤2且x≠1}
D.{x|x≥0且x≠1} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a
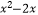 (a>0,且a≠1),x∈[0,
(a>0,且a≠1),x∈[0,  ]的最大值比最小值大2a,则a= .
]的最大值比最小值大2a,则a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=-
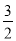 n2+
n2+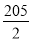 n,求数列{|an|}的前n项和Tn.
n,求数列{|an|}的前n项和Tn. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
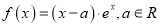 .
. (1)当
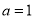 时,试求
时,试求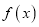 的单调增区间;
的单调增区间;(2)试求
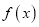 在
在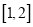 上的最大值;
上的最大值;(3)当
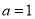 时,求证:对于
时,求证:对于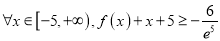 恒成立.
恒成立.
相关试题

