【题目】已知数列{an}的前n项和Sn=-![]() n2+
n2+![]() n,求数列{|an|}的前n项和Tn.
n,求数列{|an|}的前n项和Tn.
参考答案:
【答案】
【解析】试题分析:由Sn=-![]() n2+
n2+![]() n可得
n可得![]() ,故可得当当n≤34时,an>0;当n≥35时,an<0,分两种情况求数列{|an|}的前n项和Tn
,故可得当当n≤34时,an>0;当n≥35时,an<0,分两种情况求数列{|an|}的前n项和Tn
试题解析:
当n≥2时, ![]() ,
,
an=Sn-Sn-1=-3n+104.
又![]() 时,a1=S1=-
时,a1=S1=-![]() ×12+
×12+![]() ×1=101,满足上式,
×1=101,满足上式,
∴数列{an}的通项公式为an=-3n+104(n∈N*).
由an=-3n+104≥0,得n≤34.7.
即当n≤34时,an>0;当n≥35时,an<0
①当n≤34时,
Tn=|a1|+|a2|+…+|an|
=a1+a2+…+an
=Sn=-![]() n2+
n2+![]() n.
n.
②当n≥35时,
Tn=|a1|+|a2|+…+|a34|+|a35|+…+|an|
=(a1+a2+…+a34)-(a35+a36+…+an)
=2(a1+a2+…+a34)-(a1+a2+…+an)
=2S34-Sn
=2![]() -
-![]()
=![]() n2-
n2-![]() n+3502.
n+3502.
综上Tn=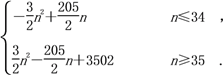
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=5
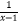 +
+ 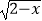 的定义域为( )
的定义域为( )
A.{x|1<x≤2}
B.{x|1≤x≤2}
C.{x|x≤2且x≠1}
D.{x|x≥0且x≠1} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a
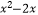 (a>0,且a≠1),x∈[0,
(a>0,且a≠1),x∈[0,  ]的最大值比最小值大2a,则a= .
]的最大值比最小值大2a,则a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+
 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ,1]上的值域.
,1]上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
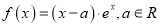 .
. (1)当
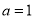 时,试求
时,试求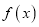 的单调增区间;
的单调增区间;(2)试求
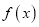 在
在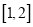 上的最大值;
上的最大值;(3)当
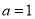 时,求证:对于
时,求证:对于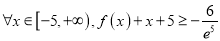 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,(1)已知a=
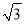 ,b=
,b=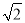 ,B=45°,求A、C、c;
,B=45°,求A、C、c;(2)已知sin A∶sin B∶sin C=(
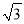 +1)∶(
+1)∶(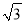 -1)∶
-1)∶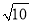 ,求最大角.
,求最大角.
相关试题

