【题目】设函数![]() .
.
(1)当![]() 时,试求
时,试求![]() 的单调增区间;
的单调增区间;
(2)试求![]() 在
在![]() 上的最大值;
上的最大值;
(3)当![]() 时,求证:对于
时,求证:对于![]() 恒成立.
恒成立.
参考答案:
【答案】(1) ![]() ;(2)详见解析; (3)详见解析.
;(2)详见解析; (3)详见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,
, ![]() ,当
,当![]() ,得
,得![]() ,所以
,所以![]() 的单调增区间为
的单调增区间为![]() ;(2)
;(2)![]() ,
, ![]() ,得
,得![]() ,讨论
,讨论![]() ,
, ![]() ,
, ![]() ,利用函数在区间
,利用函数在区间![]() 上的单调性可以求出函数
上的单调性可以求出函数![]() 在
在![]() 上的最大值;(3)当
上的最大值;(3)当![]() 时,设函数
时,设函数![]() ,则问题转化为证明对于
,则问题转化为证明对于![]() ,
, ![]() ,利用导数研究函数
,利用导数研究函数![]() 在区间
在区间![]() 的单调性,从而证明
的单调性,从而证明![]() 成立,于是问题得证.
成立,于是问题得证.
试题解析:(1)由![]() ,得
,得![]() .当
.当![]() 时,
时, ![]() ,令
,令![]() ,得
,得![]() .所以
.所以![]() 的单调增区间为
的单调增区间为![]() .
.
(2)令![]() ,得
,得![]() ,所以当
,所以当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减; ![]() 时,
时, ![]() ,
, ![]() 单调递增,综上,无论
单调递增,综上,无论![]() 为何值,当
为何值,当![]() 时,
时, ![]() 最大值都为
最大值都为![]() 或
或![]() .
. ![]() ,
,
![]() ,所以当
,所以当
![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
(3)令![]() ,所以
,所以![]() ,所以
,所以![]() ,令
,令![]() ,
,
解得![]() ,所以当
,所以当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,所以当
单调递增,所以当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() 恒成立.
恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+
 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ,1]上的值域.
,1]上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=-
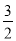 n2+
n2+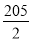 n,求数列{|an|}的前n项和Tn.
n,求数列{|an|}的前n项和Tn. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,(1)已知a=
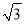 ,b=
,b=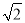 ,B=45°,求A、C、c;
,B=45°,求A、C、c;(2)已知sin A∶sin B∶sin C=(
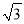 +1)∶(
+1)∶(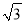 -1)∶
-1)∶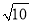 ,求最大角.
,求最大角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
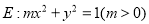 .
.(1)若椭圆
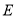 的右焦点坐标为
的右焦点坐标为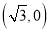 ,求
,求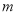 的值;
的值;(2)由椭圆
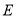 上不同三点构成三角形称为椭圆的内接三角形.若以
上不同三点构成三角形称为椭圆的内接三角形.若以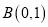 为直角顶点的椭圆
为直角顶点的椭圆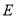 的内接等腰直角三角形恰有三个,求
的内接等腰直角三角形恰有三个,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a+1)x+(a2﹣5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
相关试题

