【题目】已知函数f(x)=a ![]() (a>0,且a≠1),x∈[0,
(a>0,且a≠1),x∈[0, ![]() ]的最大值比最小值大2a,则a= .
]的最大值比最小值大2a,则a= .
参考答案:
【答案】![]()
【解析】解:函数f(x)=a ![]() (a>0,且a≠1),x∈[0,
(a>0,且a≠1),x∈[0, ![]() ],
],
当a>1时,函数f(x)在[0,1]为减函数,在[1, ![]() ]为增函数,
]为增函数,
∴f(x)min=f(1)= ![]() ,f(x)max=f(0)=1,
,f(x)max=f(0)=1,
∴1﹣ ![]() =2a,
=2a,
即2a2﹣a+1=0,此方程无解,
当0<a<1时,函数f(x)在[0,1]为增函数,在[1, ![]() ]为减函数,
]为减函数,
∴f(x)max=f(1)= ![]() ,f(x)min=f(0)=1,
,f(x)min=f(0)=1,
∴ ![]() ﹣1=2a,
﹣1=2a,
即2a2+a﹣1=0,
解得a= ![]() 或a=﹣1(舍去),
或a=﹣1(舍去),
所以答案是: ![]() .
.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位附近只有甲、乙两个临时停车场,它们各有
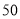 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:时间
停车场
 点
点 点
点 点
点 点
点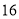 点
点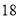 点
点甲停车场

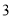

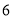
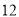
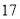
乙停车场
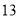
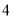
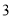
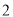

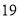
如果表中某一时刻剩余停车位数低于该停车场总车位数的
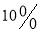 ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
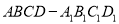 中,侧面
中,侧面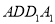 和侧面
和侧面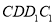 都是矩形,
都是矩形, 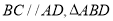 是边长为
是边长为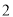 的正三角形,
的正三角形, 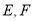 分别为
分别为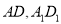 的中点.
的中点.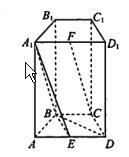
(1)求证:
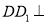 平面
平面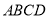 ;
;(2)求证:平面
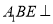 平面
平面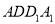 .
.(3)若
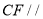 平面
平面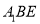 ,求棱
,求棱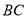 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=5
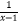 +
+ 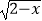 的定义域为( )
的定义域为( )
A.{x|1<x≤2}
B.{x|1≤x≤2}
C.{x|x≤2且x≠1}
D.{x|x≥0且x≠1} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+
 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ,1]上的值域.
,1]上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=-
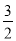 n2+
n2+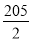 n,求数列{|an|}的前n项和Tn.
n,求数列{|an|}的前n项和Tn. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围.
相关试题

