【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,
为正三角形,![]() 为线段
为线段![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
参考答案:
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,根据中位线可得
,根据中位线可得![]() ,在根据垂直关系可证得
,在根据垂直关系可证得![]() ;根据面面平行的判定定理可证得平面
;根据面面平行的判定定理可证得平面![]()
![]() ;利用面面平行性质定理证得结论;(Ⅱ)根据线面垂直判定定理可证得
;利用面面平行性质定理证得结论;(Ⅱ)根据线面垂直判定定理可证得![]() 平面
平面![]() ,从而可以以
,从而可以以![]() 为坐标原点建立空间直角坐标系,利用线面角的向量求法可求得结果.
为坐标原点建立空间直角坐标系,利用线面角的向量求法可求得结果.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,如图所示:
,如图所示:

![]() 分别为
分别为![]() 中点
中点 ![]()
![]() 为等边三角形
为等边三角形 ![]()
又![]()
![]()
又![]()
![]() 平面
平面![]() 平面
平面![]()
又![]() 平面
平面![]()
![]() 平面
平面![]()
(Ⅱ)![]() 为正三角形,
为正三角形,![]() ,
,![]()
![]() ,
,![]()
连接![]() ,
,![]() ,则
,则![]() 为
为![]() 的中点
的中点
![]() ,
,![]()
又![]() ,
,![]()
![]()
又![]()
![]() 平面
平面![]()
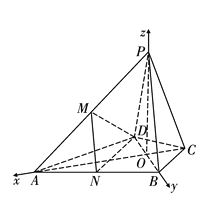
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,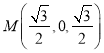
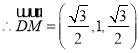 ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
 ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
则直线![]() 与平面
与平面![]() 所成角的正弦值为:
所成角的正弦值为: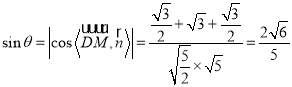
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,函数
,函数 .
.(1)若
 无零点,求实数
无零点,求实数 的取值范围;
的取值范围;(2)若
 有两个相异零点
有两个相异零点 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知椭圆
中,已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.(1)求
 的方程;
的方程;(2)过
 的左焦点
的左焦点 且斜率不为
且斜率不为 的直线
的直线 与
与 相交于
相交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 ,直线
,直线 与直线
与直线 相交于点
相交于点 ,若
,若 为等腰直角三角形,求
为等腰直角三角形,求 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个2×2的列联表;
(2)试判断能否有99.5%的把握认为“考试成绩与班级有关”?参考公式:

 ;n=a+b+c+d
;n=a+b+c+dP(
 >k)
>k)0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在
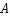 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中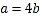 .
.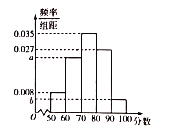
(1)求
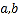 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)(2)若按照分层抽样从
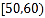 ,
, 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在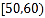 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 过点
过点 ,且离心率为
,且离心率为 .
.
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过点
 作斜率分别为
作斜率分别为 的两条直线,分别交椭圆于点
的两条直线,分别交椭圆于点 ,
, ,且
,且 ,求直线
,求直线 过定点的坐标.
过定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面 是正方形,顶点
是正方形,顶点 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为 ,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式: )
)A. 2B.
 C. 4D.
C. 4D. 
相关试题

