【题目】已知椭圆![]() 和双曲线
和双曲线![]() 有共同的焦点
有共同的焦点![]() ,
,![]() ,点
,点![]() 是
是![]() ,
,![]() 的交点,若
的交点,若![]() 是锐角三角形,则椭圆
是锐角三角形,则椭圆![]() 离心率
离心率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
设∠F1PF2=θ,则![]() ,得出
,得出![]() ,利用椭圆和双曲线的焦点三角形的面积公式可得出
,利用椭圆和双曲线的焦点三角形的面积公式可得出![]() ,结合c=2,可得出
,结合c=2,可得出![]() ,然后将椭圆和双曲线的方程联立,求出交点P的横坐标,利用该点的横坐标位于区间(﹣c,c),得出
,然后将椭圆和双曲线的方程联立,求出交点P的横坐标,利用该点的横坐标位于区间(﹣c,c),得出![]() ,可得出
,可得出![]() ,从而得出椭圆C1的离心率e的取值范围.
,从而得出椭圆C1的离心率e的取值范围.
解:设∠F1PF2=θ,则![]() ,所以,
,所以,![]() ,则
,则![]() ,
,
由焦点三角形的面积公式可得![]() ,所以,
,所以,![]() ,
,
双曲线的焦距为4,椭圆的半焦距为c=2,则b2=a2﹣c2=a2﹣4>3,
得![]() ,所以,椭圆C1的离心率
,所以,椭圆C1的离心率![]() .
.
联立椭圆C1和双曲线C2的方程 ,
,
得![]() ,得
,得![]() ,
,
由于△PF1F2为锐角三角形,则点P的横坐标![]() ,则
,则![]() ,所以,
,所以,![]() .
.
因此,椭圆C1离心率e的取值范围是![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,平面PAD⊥底面 ABCD,侧棱PA=PD=
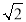 ,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.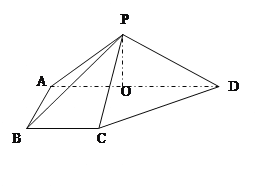
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)线段AD上是否存在点
 ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为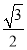 ?若存在,求出
?若存在,求出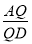 值;若不存在,请说明理由.
值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形
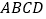 ,
,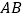 在
在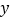 轴上且
轴上且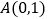 ,
,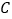
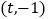 (
(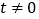 ,
,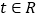 ).
). (Ⅰ)求
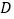 点轨迹
点轨迹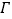 的方程;
的方程;(Ⅱ)延长
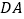 交轨迹
交轨迹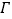 于点
于点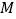 ,轨迹
,轨迹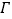 在点
在点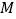 处的切线与直线
处的切线与直线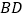 交于点
交于点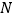 ,试判断以
,试判断以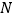 为圆心,线段
为圆心,线段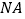 为半径的圆与直线
为半径的圆与直线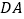 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.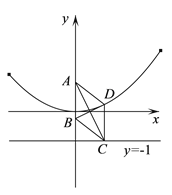
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,且质量指标值大于或等于
 的产品为优质产品.现用两种新配方(分别称为
的产品为优质产品.现用两种新配方(分别称为 配方和
配方和 配方)做试验,各生产了
配方)做试验,各生产了 件这种产品,并测量了每件产品的质量指标值(都在区间
件这种产品,并测量了每件产品的质量指标值(都在区间 内),将这些数据分成
内),将这些数据分成 组:
组: ,
, ,
, ,
, ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
已知这
 种配方生产的产品利润
种配方生产的产品利润 (单位:百元)与其质量指标值
(单位:百元)与其质量指标值 的关系式均为
的关系式均为 .
.若以上面数据的频率作为概率,分别从用
 配方和
配方和 配方生产的产品中随机抽取一件,且抽取的这
配方生产的产品中随机抽取一件,且抽取的这 件产品相互独立,则抽得的这两件产品利润之和为
件产品相互独立,则抽得的这两件产品利润之和为 的概率为( )
的概率为( )A.
 B.
B. 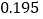 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度
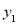 与时间t满足关系式:
与时间t满足关系式: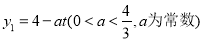 ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度 与时间t满足关系式:
与时间t满足关系式: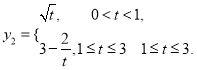 现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中,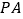 ⊥底面
⊥底面 ,
, 是
是 的中点.
的中点.已知
 ,
, ,
, ,
, .求:
.求:(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为 ,满足
,满足 .
.(1) 求角
 的大小;
的大小;(2) 若
 ,求
,求 ,
, 的值.(其中
的值.(其中 )
)
相关试题

