【题目】设![]() 为数列
为数列![]() 的前
的前![]() 项和,对任意的
项和,对任意的![]() ,都有
,都有![]() (
(![]() 为正常数).
为正常数).
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)利用![]() 与
与![]() 之间的关系
之间的关系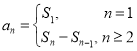 ,对
,对![]() 分两种情况讨论,
分两种情况讨论,![]() 时,求
时,求![]() 的值,
的值,![]() 时,利用
时,利用![]() 得出
得出![]() 与
与![]() 之间的关系,进而利用定义证明数列
之间的关系,进而利用定义证明数列![]() 为等比数列;
为等比数列;
(2)在(1)的条件下求出![]() 的值,然后根据数列
的值,然后根据数列![]() 的递推公式的结构利用倒数法得到数列
的递推公式的结构利用倒数法得到数列![]() 为等差数列,通过求处等差数列
为等差数列,通过求处等差数列![]() 的通项公式求出数列
的通项公式求出数列![]() 的通项公式;(3)利用(2)中数列
的通项公式;(3)利用(2)中数列![]() 的通项公式,并根据数列
的通项公式,并根据数列![]() 的通项公式的结构选择错位相减法求数列
的通项公式的结构选择错位相减法求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)证明:当![]() 时,
时,![]() ,解得
,解得![]() . 1分
. 1分
当![]() 时,
时,![]() .即
.即![]() . 2分
. 2分
又![]() 为常数,且
为常数,且![]() ,∴
,∴![]() . 3分
. 3分
∴数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列. 4分
的等比数列. 4分
(2)![]() 5分 ∵
5分 ∵![]() ,∴
,∴![]()
![]() ,即
,即![]() . 7分
. 7分
∴![]() 是首项为
是首项为![]() ,公差为1的等差数列. 8分
,公差为1的等差数列. 8分
∴![]() ,即
,即![]() . 9分
. 9分
(3)由(2)知![]() ,则
,则![]() .
.
所以![]() , 10分
, 10分
即![]() , ① 11分
, ① 11分
则![]() , ② 12分
, ② 12分
②-①得![]() , 13分
, 13分
故![]() . 14分
. 14分
-
科目: 来源: 题型:
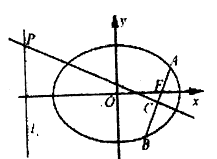
查看答案和解析>>【题目】如图,在平面直角坐标系
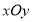 中,已知椭圆
中,已知椭圆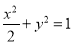 ,直线
,直线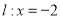 ,过右焦点
,过右焦点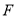 的直线与椭圆交于
的直线与椭圆交于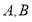 两点,线段
两点,线段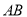 的垂直平分线分别交直线
的垂直平分线分别交直线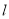 和
和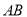 于点
于点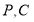 .
.
(1)求弦长
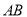 的最小值;
的最小值;(2)在直线
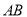 上任取一点
上任取一点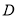 ,当
,当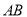 的斜率
的斜率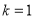 时,求
时,求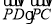 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.

(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位有200名职工,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是 ( )
A.由五个平面围成的多面体只能是四棱锥
B.棱锥的高线可能在几何体之外
C.仅有一组对面平行的六面体是棱台
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤ x ≤80时,每天售出的件数为P=
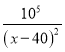 ,每天获得的利润为y(元)
,每天获得的利润为y(元)(1)写出关于x的函数y的表达式;
(2)若想每天获得的利润最多,问售价应定为每件多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量
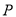 (件)与单价
(件)与单价 (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(1)根据周销售量图写出
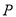 (件)与单价
(件)与单价 (元)之间的函数关系式;
(元)之间的函数关系式;(2)写出利润
 (元)与单价
(元)与单价 (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
相关试题

