【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,若
时,若![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅲ)若对任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(Ⅰ)把a=1代入函数解析式,求导后求出f′(1),同时求出f(1),由点斜式写出切线方程;
(Ⅱ)求出函数的定义域,求出原函数的导函数![]() ,进一步求出导函数的零点
,进一步求出导函数的零点![]() ,分
,分![]() 和
和![]() 三种情况讨论三种情况讨论原函数的单调性,由f(x)在区间[1,e]上的最小值为-2求解
三种情况讨论三种情况讨论原函数的单调性,由f(x)在区间[1,e]上的最小值为-2求解![]() 的取值范围;
的取值范围;
(Ⅲ)构造辅助函数g(x)=f(x)+2x,问题转化为函数g(x)在(0,+∞)上单调递增,求解![]() 的范围.把函数g(x)求导后分
的范围.把函数g(x)求导后分![]() =0和
=0和![]() ≠0讨论,
≠0讨论, ![]() ≠0时借助于二次函数过定点及对称轴列式求解.
≠0时借助于二次函数过定点及对称轴列式求解.
试题解析:
(1)由![]() ,则
,则![]()
![]() ,所以切线方程为
,所以切线方程为![]()
(2)![]()
令![]()
![]()
当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]()
当![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减, ![]()
![]() (舍)
(舍)
当![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() (舍)
(舍)
综上, ![]()
(3)令![]()
![]()
令![]() ,只要
,只要![]() 在
在![]() 上单调递增即可.
上单调递增即可.
![]() 在
在![]() 上恒成立.
上恒成立.
![]()
![]()
![]() 在
在![]() 上恒成立.
上恒成立.
当![]() 时,
时, ![]() 恒成立;
恒成立;
当![]() 时,原不等式
时,原不等式![]()
当时,原不等式![]() ,左边无最大值,不合题意(舍)
,左边无最大值,不合题意(舍)
综上, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程(x2﹣2x+m)(x2﹣2x+n)=0的四个根组成一个首项为
 的等差数列,则|m﹣n|等于( )
的等差数列,则|m﹣n|等于( )
A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设公差大于0的等差数列
 成等比数列,记数列
成等比数列,记数列 的前n项和为
的前n项和为 .
.(Ⅰ)求
 ;
;(Ⅱ)若对于任意的n∈
 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某工艺厂有铜丝5万米,铁丝9万米,准备用这两种材料编制成花篮和花盆出售,已知一只花篮需要用铜丝200米,铁丝300米;编制一只花盆需要100米,铁丝300米,设该厂用所有原来编制个花篮
 ,
,  个花盆.
个花盆.(Ⅰ)列出
 满足的关系式,并画出相应的平面区域;
满足的关系式,并画出相应的平面区域;(Ⅱ)若出售一个花篮可获利300元,出售一个花盘可获利200元,那么怎样安排花篮与花盆的编制个数,可使得所得利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“a≥3
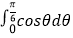 ”是“直线l:2ax﹣y+2a2=0(a>0)与双曲线C:
”是“直线l:2ax﹣y+2a2=0(a>0)与双曲线C: 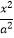 ﹣
﹣ 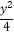 =1的右支无交点”的( )
=1的右支无交点”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, 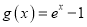 ,其中
,其中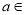 R,
R,  …为自然对数的底数.
…为自然对数的底数.(Ⅰ)当
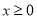 时,
时, 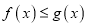 恒成立,求
恒成立,求 的取值范围;
的取值范围;(Ⅱ)求证:
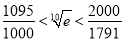 (参考数据:
(参考数据:  ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意实数x,cos2x+2ksinx﹣2k﹣2<0恒成立,则实数k的取值范围是( )
A.
B.
C.
D.k>﹣1
相关试题

