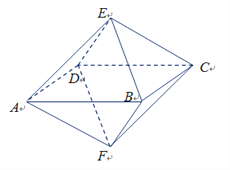
【题目】如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是
A. 不平行的两条棱所在直线所成的角为![]() 或
或![]() B. 四边形AECF为正方形
B. 四边形AECF为正方形
C. 点A到平面BCE的距离为![]() D. 该八面体的顶点在同一个球面上
D. 该八面体的顶点在同一个球面上
参考答案:
【答案】C
【解析】解答:
因为八面体的各条棱长均为1,四边形ABCD为正方形,
所以在四棱锥EABCD中,相邻两条侧棱所成的角为60°,而像AE与CE所成的角为90°,A正确;
因为AE=CE=1,AC=![]() ,满足勾股定理的逆定理,所以AE⊥CE,同理AF⊥CF,AE⊥AF,所以四边形AECF是正方形;故B正确;
,满足勾股定理的逆定理,所以AE⊥CE,同理AF⊥CF,AE⊥AF,所以四边形AECF是正方形;故B正确;
设点A到平面BCE的距离h,由VEABCD=2VABCE,
所以![]() ;
;
所以点A到平面BCE的距离![]() ;故C错误;
;故C错误;
该八面体的顶点会在同一个球面上,球心为ABCD的中心,故D正确。
本题选择C选项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
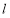 的参数方程为
的参数方程为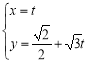 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系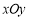 的
的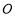 点为极点,
点为极点,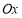 方向为极轴,选择相同的长度单位建立极坐标系,得曲线
方向为极轴,选择相同的长度单位建立极坐标系,得曲线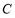 的极坐标方程为
的极坐标方程为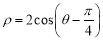 .
.(1)求直线
 的倾斜角和曲线
的倾斜角和曲线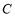 的直角坐标方程;
的直角坐标方程;(2)若直线
 与曲线
与曲线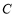 交于
交于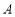 、
、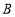 两点,设点
两点,设点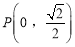 ,求
,求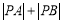 .
. -
科目: 来源: 题型:
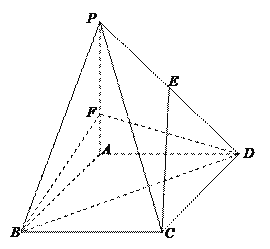
查看答案和解析>>【题目】如图,在边长为3的菱形ABCD中,∠ABC=60°,
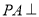 平面ABCD,且
平面ABCD,且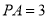 ,E为PD中点,F在棱PA上,且
,E为PD中点,F在棱PA上,且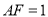 .
.(1)求证:CE∥平面BDF;
(2)求点P到平面BDF的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
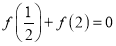 ,求
,求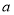 的值;
的值;(2)若存在
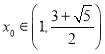 ,使函数
,使函数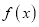 的图像在点
的图像在点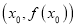 和点
和点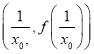 处的切线互相垂直,求
处的切线互相垂直,求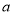 的取值范围;
的取值范围;(3)若函数
 在区间
在区间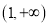 上有两个极值点,则是否存在实数
上有两个极值点,则是否存在实数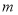 ,使
,使 对任意的
对任意的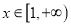 恒成立?若存在,求出
恒成立?若存在,求出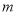 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
-
科目: 来源: 题型:
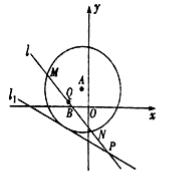
查看答案和解析>>【题目】如图所示,已知圆
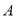 的圆心在直线
的圆心在直线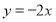 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线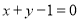 对称,又圆
对称,又圆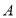 与直线
与直线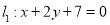 相切,过点
相切,过点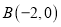 的动直线
的动直线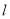 与圆
与圆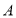 相交于
相交于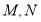 两点,
两点,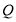 是
是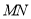 的中点,直线
的中点,直线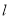 与
与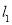 相交于点
相交于点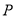 .
.
(1)求圆
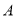 的方程;
的方程;(2)当
 时,求直线
时,求直线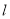 的方程;
的方程;(3)
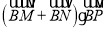 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
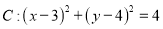 ,直线
,直线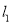 经过点A (1,0).
经过点A (1,0).(1)若直线
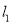 与圆C相切,求直线
与圆C相切,求直线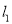 的方程;
的方程; (2)若直线
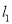 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线 的方程.
的方程.
相关试题

