【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.
(1)求数列{bn}的通项公式;
(2)令cn=![]() ,Tn是数列{cn}的前n项和,求证:
,Tn是数列{cn}的前n项和,求证:![]()
参考答案:
【答案】(1)bn=3n+1;(2)见解析.
【解析】试题分析:(1)求等比数列的通项公式,关键是求出首项和公比,这可直接用首项![]() 和公比
和公比![]() 表示出已知并解出即可(可先把已知化简后再代入);(2)求出
表示出已知并解出即可(可先把已知化简后再代入);(2)求出![]() 的表达式后,用错位相减法求其前
的表达式后,用错位相减法求其前![]() 项和,然后求其最小值即可得结论.
项和,然后求其最小值即可得结论.
试题解析:(1) 由题意知,当n≥2时,an=Sn-Sn-1=6n+5;当n=1时,a1=S1=11,也符合上式,所以an=6n+5.
设数列{bn}的公差为d.由![]() 即
即![]() 解得
解得![]()
所以bn=3n+1.
(2) 由(1)知cn=![]() =3(n+1)·2n+1.
=3(n+1)·2n+1.
又Tn=c1+c2+…+cn,
得Tn=3×[2×22+3×23+…+(n+1)×2n+1],
2Tn=3×[2×23+3×24+…+(n+1)×2n+2],
两式作差,得
-Tn=3×[2×22+23+24+…+2n+1-(n+1)×2n+2]
=3×[4+![]() -(n+1)×2n+2]=-3n·2n+2,
-(n+1)×2n+2]=-3n·2n+2,
所以Tn=3n·2n+2.
![]()
【 方法点睛】本题主要考查等差数列的通项以及错位相减法求数列的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列,![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”
”![]() 与“
与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
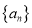 是首项为0的递增数列,
是首项为0的递增数列,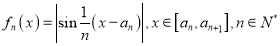 ,满足:对于任意的
,满足:对于任意的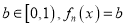 总有两个不同的根,则
总有两个不同的根,则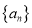 的通项公式为_________
的通项公式为_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆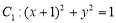 ,圆
,圆 .
.(1)若过点
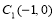 的直线
的直线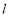 被圆
被圆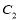 截得的弦长为
截得的弦长为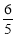 ,求直线
,求直线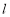 的方程;
的方程;(2)圆
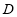 是以1为半径,圆心在圆
是以1为半径,圆心在圆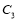 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆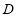 上任意一点
上任意一点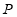 分别作圆
分别作圆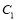 的两条切线
的两条切线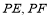 ,切点为
,切点为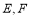 ,求
,求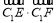 的取值范围;
的取值范围;(3)若动圆
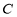 同时平分圆
同时平分圆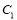 的周长、圆
的周长、圆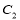 的周长,则动圆
的周长,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
, ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(I)求直方图中
 的值;
的值; (II)求月平均用电量的众数和中位数;
(III)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 ,底面
,底面 是
是 、边长为
、边长为 的菱形,又
的菱形,又 底
底 ,且
,且 ,点
,点 分别是棱
分别是棱 的中点.
的中点.
(1)证明:
 平面
平面 ;
;(2)证明:平面
 平面
平面 ;
;(3)求点
 到平面
到平面 的距离.[
的距离.[ -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 的棱长为1,
的棱长为1,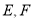 分别是棱
分别是棱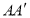 ,
, 的中点,过直线
的中点,过直线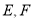 的平面分别与棱
的平面分别与棱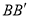 、
、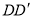 交于
交于 ,设
,设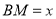 ,
,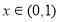 ,给出以下四个命题:
,给出以下四个命题:①四边形
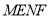 为平行四边形;
为平行四边形;②若四边形
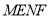 面积
面积 ,
,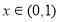 ,则
,则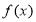 有最小值;
有最小值;③若四棱锥
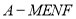 的体积
的体积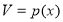
 ,
,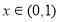 ,则
,则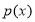 为常函数;
为常函数;④若多面体
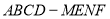 的体积
的体积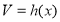 ,
,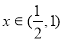 ,则
,则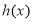 为单调函数.
为单调函数.其中假命题为( )
A.① ③ B.② C.③④ D.④
相关试题

