【题目】已知函数f(x)=x2﹣cosx,x∈[﹣ ![]() ,
, ![]() ],则满足f(x0)>f(
],则满足f(x0)>f( ![]() )的x0的取值范围为 .
)的x0的取值范围为 .
参考答案:
【答案】[﹣ ![]() ,﹣
,﹣ ![]() )∪(
)∪( ![]() ,
,![]() ]
]
【解析】解:注意到函数f(x)=x2﹣cosx,x∈[﹣ ![]() ,
, ![]() ]是偶函数,
]是偶函数,
故只需考虑[0, ![]() ]区间上的情形.
]区间上的情形.
当x∈[0, ![]() ]时,f′(x)=2x+sinx≥0,
]时,f′(x)=2x+sinx≥0,
∴函数在[0, ![]() ]单调递增,
]单调递增,
所以f(x0)>f( ![]() )在[0,
)在[0, ![]() ]上的解集为(
]上的解集为( ![]() ,
, ![]() ],
],
结合函数是偶函数,图象关于y轴对称,
得原问题中x0取值范围是[﹣ ![]() ,﹣
,﹣ ![]() )∪(
)∪( ![]() ,
, ![]() ],
],
所以答案是:[﹣ ![]() ,﹣
,﹣ ![]() )∪(
)∪( ![]() ,
, ![]() ].
].
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值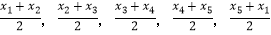 的概率均为
的概率均为 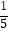 ,随机变量Y取值
,随机变量Y取值 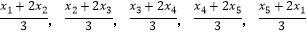 的概率也均为
的概率也均为 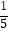 ,比较DX与DY大小关系.
,比较DX与DY大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】近来景德镇市棚户区改造进行的如火如荼,加上城市人居环境的不断改善,我市房地产住宅销售价格节节攀升,一部分刚需住户带来了不小的烦恼,下表为我市2017.1﹣2017.5这5月住宅价格与月份的关系.
月份x
1
2
3
4
5
住宅价格y
千元/平米4.8
5.4
6.2
6.6
7
(1)通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度(精确到0.01)
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系. ①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(m-1,2),B(1,1),C(3,m2-m-1).
(1)若A,B,C三点共线,求实数m的值;
(2)若AB⊥BC,求实数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正实数x,y,z满足x+y+z=1,
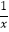 +
+ 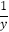 +
+  =10,则xyz的最大值为 .
=10,则xyz的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中,  分别为
分别为 的中点,点
的中点,点 为线段
为线段 上的一点,将
上的一点,将 沿
沿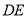 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.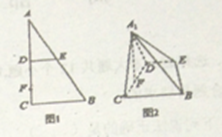
(1)求证:
 ;
;(2)线段
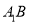 上是否存在点
上是否存在点 ,使
,使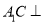 平面
平面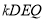 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数
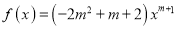 为偶函数.
为偶函数.(1)求
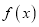 的解析式;
的解析式;(2)若函数
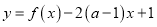 在区间
在区间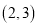 上为单调函数,求实数
上为单调函数,求实数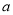 的取值范围.
的取值范围.
相关试题

