【题目】如图,在直三棱柱![]() 中,点
中,点![]() 分别在棱
分别在棱![]() 上(均异于端点),且
上(均异于端点),且![]() .
.
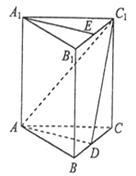
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1) 利用面面垂直的判定定理,只需证明一个平面经过另一个平面的垂直,证明![]() 平面
平面![]() 即可;(2 )利用线面平行的判定定理,只需证明平面外的直线平行于平面内的一条直线,证明
即可;(2 )利用线面平行的判定定理,只需证明平面外的直线平行于平面内的一条直线,证明![]() 即可.
即可.
试题解析: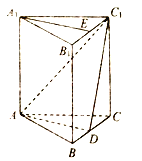
(1)在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)因为![]() ,由(1)同理可得,
,由(1)同理可得, ![]() 平面
平面![]() ,
,
又由(1)知, ![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的判定定理,属于中档题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
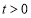 ,设函数
,设函数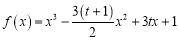 .
.(1)存在
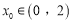 ,使得
,使得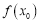 是
是 在
在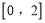 上的最大值,求
上的最大值,求 的取值范围;
的取值范围;(2)
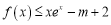 对任意
对任意 恒成立时,
恒成立时,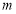 的最大值为1,求
的最大值为1,求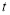 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
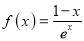 .
.(Ⅰ)求曲线
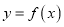 在点
在点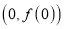 处的切线方程和函数
处的切线方程和函数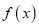 的极值;
的极值;(Ⅱ)若对任意的
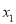 ,
, 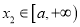 ,都有
,都有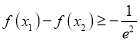 成立,求实数
成立,求实数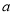 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂2万元设计了某款式的服装,根据经验,每生产1百套该款式服装的成本为1万元,每生产
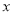 (百套)的销售额(单位:万元)
(百套)的销售额(单位:万元)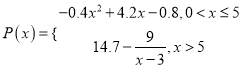 .
.(1)若生产6百套此款服装,求该厂获得的利润;
(2)该厂至少生产多少套此款式服装才可以不亏本?
(3)试确定该厂生产多少套此款式服装可使利润最大,并求最大利润.(注:利润=销售额-成本,其中成本=设计费+生产成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
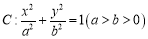 的左、右焦点分别为
的左、右焦点分别为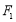 、
、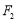 ,上顶点为
,上顶点为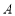 ,过
,过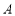 与
与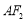 垂直的直线交
垂直的直线交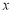 轴负半轴于
轴负半轴于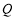 点,且
点,且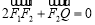 .
.(1)求椭圆
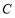 的离心率;
的离心率;(2)若过
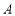 、
、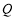 、
、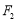 三点的圆恰好与直线
三点的圆恰好与直线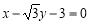 相切,求椭圆
相切,求椭圆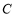 的方程;
的方程;(3)过
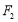 的直线
的直线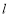 与(2)中椭圆交于不同的两点
与(2)中椭圆交于不同的两点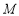 、
、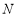 ,则
,则 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平面
平面 ,
,  ,
,  ,
,  ,
,  为
为 的中点.
的中点.
(Ⅰ)证明:
 平面
平面 ;
;(Ⅱ)求多面体
 的体积;
的体积;(Ⅲ)求二面角
 的正切值.
的正切值. -
科目: 来源: 题型:
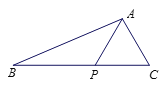
查看答案和解析>>【题目】如图, 在△
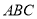 中, 点
中, 点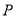 在
在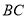 边上,
边上, 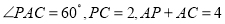 .
.(Ⅰ)求
 ;
;(Ⅱ)若△
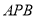 的面积是
的面积是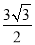 , 求
, 求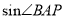 .
.
相关试题

