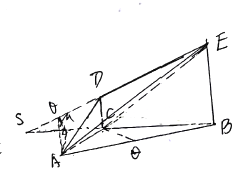
【题目】如图, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求多面体![]() 的体积;
的体积;
(Ⅲ)求二面角![]() 的正切值.
的正切值.
参考答案:
【答案】(Ⅰ)证明见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】【试题分析】(Ⅰ)先运用线面垂直的性质定理证明![]() ,再运用等腰三角形的性质证明
,再运用等腰三角形的性质证明![]() ,进而运用线面垂直的判定定理证明
,进而运用线面垂直的判定定理证明![]() 平面
平面![]() ;(Ⅱ)先求三棱锥的高
;(Ⅱ)先求三棱锥的高![]() 和底面三角形
和底面三角形![]() 面积
面积![]() ,用三棱锥的体积公式求出体积;(Ⅲ)先运用二面角平面角的定义找出二面角
,用三棱锥的体积公式求出体积;(Ⅲ)先运用二面角平面角的定义找出二面角![]() 的平面角
的平面角![]() ,再构造直角三角形
,再构造直角三角形![]() ,运用相似三角形的性质求出
,运用相似三角形的性质求出![]() ,最后运用解直角三角形的正切函数的定义求出
,最后运用解直角三角形的正切函数的定义求出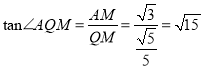 :
:
(Ⅰ)证明:∵![]() 平面
平面![]() ,
, ![]()
∴![]() 平面
平面![]()
∴![]() ①
①
又∵![]() ,点
,点![]() 为
为![]() 边中点
边中点
∴![]() ②
②
![]()
故由①②得![]() 平面
平面![]()
(Ⅱ)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]()
∵![]()
∴![]() 平面
平面![]()
∴![]()
![]() ,
, ![]()
∴![]()
(Ⅲ)延长![]() 交
交![]() 延长线于
延长线于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连结
,连结![]()
由(Ⅱ)可得: ![]() 为
为![]() 的平面角
的平面角
∵![]()
∴![]()
∴![]()
![]()
∵![]() ∽
∽![]()
∴![]()
∴![]() 即
即![]()
∴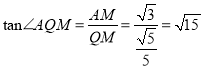
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂2万元设计了某款式的服装,根据经验,每生产1百套该款式服装的成本为1万元,每生产
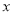 (百套)的销售额(单位:万元)
(百套)的销售额(单位:万元)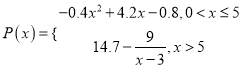 .
.(1)若生产6百套此款服装,求该厂获得的利润;
(2)该厂至少生产多少套此款式服装才可以不亏本?
(3)试确定该厂生产多少套此款式服装可使利润最大,并求最大利润.(注:利润=销售额-成本,其中成本=设计费+生产成本)
-
科目: 来源: 题型:
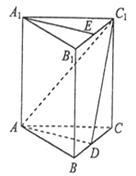
查看答案和解析>>【题目】如图,在直三棱柱
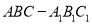 中,点
中,点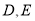 分别在棱
分别在棱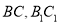 上(均异于端点),且
上(均异于端点),且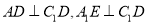 .
.
(1)求证:平面
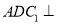 平面
平面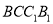 ;
;(2)求证:
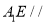 平面
平面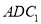 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
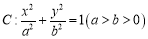 的左、右焦点分别为
的左、右焦点分别为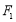 、
、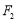 ,上顶点为
,上顶点为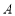 ,过
,过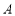 与
与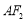 垂直的直线交
垂直的直线交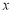 轴负半轴于
轴负半轴于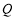 点,且
点,且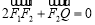 .
.(1)求椭圆
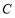 的离心率;
的离心率;(2)若过
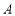 、
、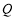 、
、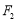 三点的圆恰好与直线
三点的圆恰好与直线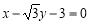 相切,求椭圆
相切,求椭圆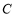 的方程;
的方程;(3)过
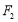 的直线
的直线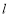 与(2)中椭圆交于不同的两点
与(2)中椭圆交于不同的两点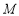 、
、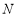 ,则
,则 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由. -
科目: 来源: 题型:
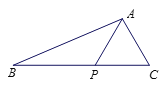
查看答案和解析>>【题目】如图, 在△
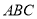 中, 点
中, 点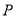 在
在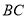 边上,
边上, 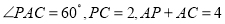 .
.(Ⅰ)求
 ;
;(Ⅱ)若△
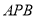 的面积是
的面积是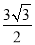 , 求
, 求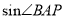 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
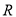 上的单调递减函数
上的单调递减函数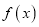 ,对任意
,对任意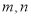 都有
都有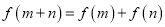 ,
,  .
.(Ⅰ)判断函数
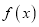 的奇偶性,并证明之;
的奇偶性,并证明之;(Ⅱ)若对任意
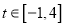 ,不等式
,不等式 (
( 为常实数)都成立,求
为常实数)都成立,求 的取值范围;(Ⅲ)设
的取值范围;(Ⅲ)设 ,
,  ,
,  ,
, 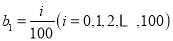 ,
,  .
.若

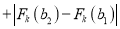
 ,
,  ,比较
,比较 的大小并说明理由.
的大小并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
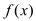 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表,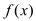 的导函数
的导函数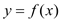 的图象如图所示,下列关于
的图象如图所示,下列关于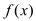 的命题:
的命题: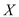
-1
0
4
5
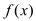
1
2
2
1
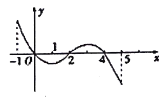
①函数
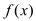 的极大值点为0,4;
的极大值点为0,4;②函数
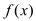 在[0,2]上是减函数;
在[0,2]上是减函数;③如果当
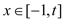 时,
时,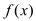 的最大值是2,那么
的最大值是2,那么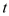 的最大值为4;
的最大值为4;④当
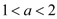 时,函数
时,函数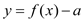 有4个零点.
有4个零点.其中正确命题的序号是__________.
相关试题

