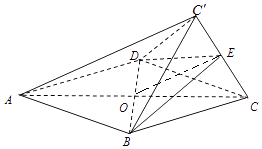
【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′= ![]() ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 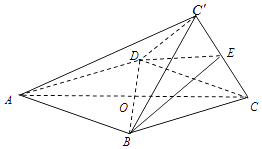
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积.
参考答案:
【答案】
(1)证明:连接OE,则在菱形ABCD中,O为AC中点,
又E为CC′的中点,∴OE∥AC′,
∵OE平面BDE,AC′平面BDE,
∴AC′∥平面BDE
(2)证明:由翻折前后可知:
BC=BC′,DC=DC′,
又E为CC′中点,∴BE⊥CC′,DE⊥CC′,
又BE∩DE=E,∴CC′⊥平面BDE
(3)解:连接OE,则由(2)知△CEO为直角三角形,OE⊥BD,
∴BD=2,OE= ![]() ,
,
∴三棱锥C′﹣BCD的体积:
![]()
= ![]()
= ![]()
= ![]()
= ![]() .
.
【解析】(1)连接OE,则OE∥AC′,由此能证明AC′∥平面BDE.(2)由翻折前后可知BE⊥CC′,DE⊥CC′,由此能证明CC′⊥平面BDE.(3)连接OE,三棱锥C′﹣BCD的体积: ![]() ,由此能求出结果.
,由此能求出结果.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
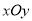 中,直线
中,直线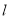 的参数方程为
的参数方程为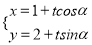 (
(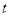 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系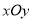 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以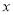 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆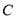 的方程为
的方程为 .
.(1)求圆
 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线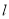 交于点
交于点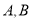 ,若点
,若点 的坐标为
的坐标为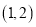 ,求
,求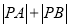 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形, ,侧面
,侧面 底面
底面 ,
, ,
, ,
,  分别为
分别为 的中点,点
的中点,点 在线段
在线段 上.
上.
(Ⅰ)求证:
 平面
平面 ;
; (Ⅱ)如果直线
 与平面
与平面 所成的角和直线
所成的角和直线 与平面
与平面 所成的角相等,求
所成的角相等,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(理)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A、B、C、D的距离都等于2.给出以下结论:
①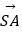 +
+ 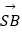 +
+ 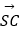 +
+ 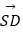 =
= 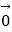 ;
;
②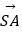 +
+ 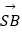 ﹣
﹣ 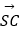 ﹣
﹣ 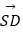 =
= 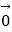 ;
;
③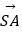 ﹣
﹣ 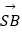 +
+ 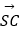 ﹣
﹣ 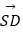 =
= 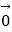 ;
;
④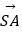
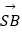 =
= 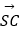
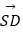 ;
;
⑤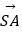
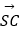 =0,
=0,
其中正确结论是( )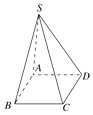
A.①②③
B.④⑤
C.②④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,q:函数f(x)=(3﹣2a)x是增函数,若p或q为真,p且q为假,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=
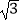 ,∠ABC=60°.
,∠ABC=60°. 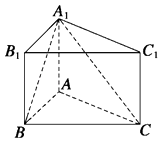
(1)证明:AB⊥A1C;
(2)(理)求二面角A﹣A1C﹣B的余弦值大小.
(文)求此棱柱的体积.
相关试题

