【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1= ![]() ,∠ABC=60°.
,∠ABC=60°. 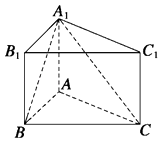
(1)证明:AB⊥A1C;
(2)(理)求二面角A﹣A1C﹣B的余弦值大小.
(文)求此棱柱的体积.
参考答案:
【答案】
(1)解:∵在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1= ![]() ,∠ABC=60°
,∠ABC=60°
∴AA1⊥AB,
∵三角形ABC中AB=1,AC= ![]() ,∠ABC=60°,
,∠ABC=60°,
∴由正弦定理得 ![]() =
= ![]() ,∠ACB=30°
,∠ACB=30°
∴∠BAC=90°,
∴AB⊥AC;
∵AA1∩AC=A
∴AB⊥面A1CA;
∵A1C面A1CA;
∴AB⊥A1C
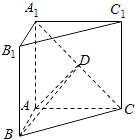
(2)解:(理)如图,作AD⊥A1C交A1C于D点,连接BD,
由三垂线定理知BD⊥A1C,
∴∠ADB为二面角A﹣A1C﹣B的平面角.
在Rt△AA1C中,AD= ![]() =
= ![]() ,
,
在Rt△BAD中,tan∠ADB= ![]() =
= ![]() ,
,
∴cos∠ADB= ![]() ,
,
即二面角A﹣A1C﹣B的余弦值为 ![]()
(文)此棱柱的体积= ![]() =
= ![]() =
= ![]()
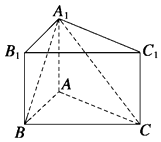
【解析】分析1)欲证AB⊥A1C,而A1C平面ACC1A1 , 可先证AB⊥平面ACC1A1 , 根据三棱柱ABC﹣A1B1C1为直三棱柱,可知AB⊥AA1 , 由正弦定理得AB⊥AC,满足线面垂直的判定定理所需条件;(2)(理)作AD⊥A1C交A1C于D点,连接BD,由三垂线定理知BD⊥A1C,则∠ADB为二面角A﹣A1C﹣B的平面角,在Rt△BAD中,求出二面角A﹣A1C﹣B的余弦值即可.(文)根据柱体的体积公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=
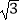 ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 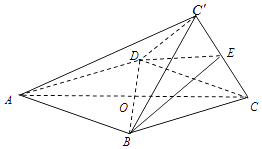
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(理)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A、B、C、D的距离都等于2.给出以下结论:
①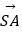 +
+ 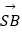 +
+ 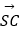 +
+ 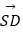 =
= 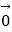 ;
;
②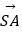 +
+ 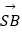 ﹣
﹣ 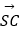 ﹣
﹣ 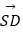 =
= 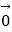 ;
;
③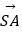 ﹣
﹣ 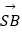 +
+ 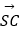 ﹣
﹣ 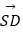 =
= 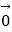 ;
;
④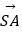
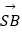 =
= 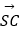
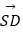 ;
;
⑤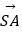
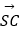 =0,
=0,
其中正确结论是( )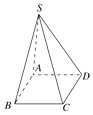
A.①②③
B.④⑤
C.②④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,q:函数f(x)=(3﹣2a)x是增函数,若p或q为真,p且q为假,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
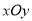 中,已知椭圆
中,已知椭圆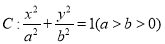 过点
过点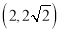 ,
, 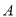 ,
, 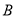 分别为椭圆
分别为椭圆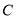 的右、下顶点,且
的右、下顶点,且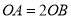 .
.(1)求椭圆
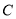 的方程;
的方程;(2)设点
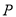 在椭圆
在椭圆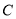 内,满足直线
内,满足直线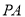 ,
, 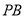 的斜率乘积为
的斜率乘积为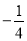 ,且直线
,且直线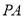 ,
, 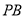 分别交椭圆
分别交椭圆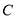 于点
于点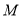 ,
, 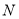 .
.(i) 若
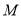 ,
, 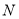 关于
关于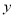 轴对称,求直线
轴对称,求直线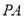 的斜率;
的斜率;(ii) 求证:
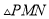 的面积与
的面积与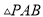 的面积相等.
的面积相等.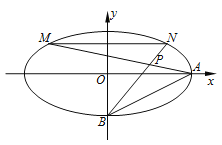
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(sinA,cosA),
=(sinA,cosA), 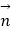 =(cosB,sinB),
=(cosB,sinB), 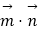 =sin2C且A、B、C分别为△ABC的三边a,b,c所对的角.
=sin2C且A、B、C分别为△ABC的三边a,b,c所对的角.
(1)求角C的大小;
(2)若sinA,sinC,sinB成等比数列,且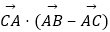 =18,求c的值..
=18,求c的值.. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一块地皮
 ,其中
,其中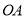 ,
, 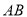 是直线段,曲线段
是直线段,曲线段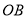 是抛物线的一部分,且点
是抛物线的一部分,且点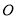 是该抛物线的顶点,
是该抛物线的顶点, 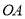 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, 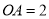 km,
km, 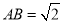 km,
km, 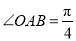 .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形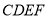 来建造草坪,其中点
来建造草坪,其中点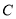 在曲线段
在曲线段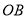 上,点
上,点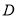 ,
, 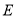 在直线段
在直线段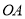 上,点
上,点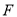 在直线段
在直线段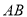 上,设
上,设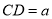 km,矩形草坪
km,矩形草坪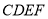 的面积为
的面积为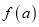 km2.
km2.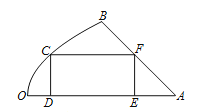
(1)求
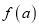 ,并写出定义域;
,并写出定义域;(2)当
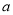 为多少时,矩形草坪
为多少时,矩形草坪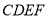 的面积最大?
的面积最大?
相关试题

