【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值.
参考答案:
【答案】
(1)解:由方程x2+y2﹣2x﹣4y+m=0变形为(x﹣1)2+(y﹣2)2=5﹣m.∵此方程表示圆,∴5﹣m>0,解得m<5,故m的取值范围是(﹣∞,5)
(2)解:设M(x1,y1),N(x2,y2).
联立 ![]() 化为5y2﹣16y+8+m=0,
化为5y2﹣16y+8+m=0,
∵直线与圆相交,∴△=162﹣20(8+m)>0,化为 ![]() .
.
∴y1+y2= ![]() ,
, ![]() .
.
∵ ![]() ,∴
,∴ ![]() =0,
=0,
又x1x2=(4﹣2y1)(4﹣2y2)=16﹣8(y1+y2)+4y1y2,
∴5y1y2﹣8(y1+y2)+16=0,
∴8+m﹣ ![]() +16=0,
+16=0,
解得m= ![]() ,满足
,满足 ![]() ,
,
故m= ![]()
【解析】(1)由方程x2+y2﹣2x﹣4y+m=0配方为(x﹣1)2+(y﹣2)2=5﹣m.由于此方程表示圆,可得5﹣m>0,解出即可;(2)设M(x1 , y1),N(x2 , y2).与圆的方程联立可得△>0及根与系数关系,再利用 ![]() ,
, ![]() =0,即可解出m.
=0,即可解出m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC1是正方体ABCD﹣A1B1C1D1的对角线.
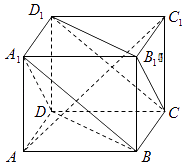
(1)求证:平面A1BD∥平面CD1B1;
(2)求证:直线AC1⊥直线BD. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3
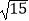 ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣  .
.
(1)求a和sinC的值;
(2)求cos(2A+ )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}与{bn},若a1=3且对任意正整数n满足an+1﹣an=2,数列{bn}的前n项和Sn=n2+an .
(1)求数列{an},{bn}的通项公式;
(2)求数列{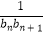 }的前n项和Tn .
}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
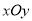 中,直线
中,直线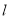 的参数方程为
的参数方程为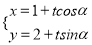 (
(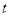 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系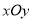 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以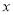 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆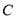 的方程为
的方程为 .
.(1)求圆
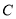 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线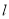 交于点
交于点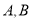 ,若点
,若点 的坐标为
的坐标为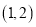 ,求
,求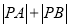 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形, ,侧面
,侧面 底面
底面 ,
, ,
, ,
,  分别为
分别为 的中点,点
的中点,点 在线段
在线段 上.
上.
(Ⅰ)求证:
 平面
平面 ;
; (Ⅱ)如果直线
 与平面
与平面 所成的角和直线
所成的角和直线 与平面
与平面 所成的角相等,求
所成的角相等,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=
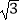 ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 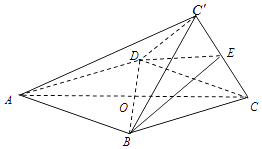
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积.
相关试题

