【题目】下列函数中,既是偶函数,又在(0,+∞)单调递增的函数是( )
A.y=﹣x2
B.y=2﹣|x|
C.y=| ![]() |
|
D.y=lg|x|
参考答案:
【答案】D
【解析】解:对于A,y=﹣x2是定义域R上的偶函数,但在(0,+∞)上单调递减,不满足题意;
对于B,y=2﹣|x|是定义域R上的偶函数,但在(0,+∞)上单调递减,不满足题意;
对于C,y=| ![]() |是定义域(﹣∞,0)∪(0,+∞)上的偶函数,在(0,+∞)上单调递减,不满足题意;
|是定义域(﹣∞,0)∪(0,+∞)上的偶函数,在(0,+∞)上单调递减,不满足题意;
对于D,y=lg|x|是定义域(﹣∞,0)∪(0,+∞)上的偶函数,且在(0,+∞)上单调递增,满足题意.
故选:D.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和函数的奇偶性的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段
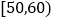 ,
,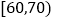 ,…,
,…,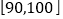 后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如图部分频率分布直方图.观察图形的信息,回答下列问题: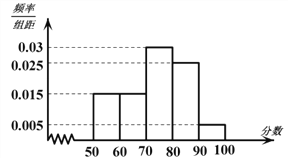
(1)求出这60名学生中化学成绩低于50分的人数;
(2)估计高二年级这次考试化学学科及格率(60分以上为及格);
(3)从化学成绩不及格的学生中随机调查1人,求他的成绩低于50分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
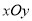 中,设椭圆
中,设椭圆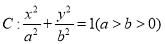 的焦点为
的焦点为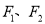 ,过右焦点
,过右焦点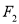 的直线
的直线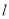 与椭圆
与椭圆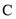 相交于
相交于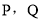 两点,若
两点,若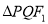 的周长为短轴长的
的周长为短轴长的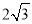 倍.
倍.(Ⅰ)求椭圆
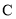 的离心率;
的离心率;(Ⅱ)设
 的斜率为
的斜率为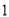 ,在椭圆
,在椭圆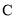 上是否存在一点
上是否存在一点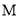 ,使得
,使得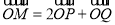 ?若存在,求出点
?若存在,求出点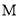 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
 +
+  的定义域为( )
的定义域为( )
A.[﹣2,0)∪(0,2]
B.(﹣1,0)∪(0,2]
C.[﹣2,2]
D.(﹣1,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次运动会中甲、乙两名射击运动员决赛中各射击十次的成绩(环)如下:

(1)用茎叶图表示甲、乙两个人的成绩;
(2)根据茎叶图分析甲、乙两人的成绩;
(3)计算两个样本的平均数
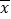 和标准差
和标准差 ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程 .
.(1)若
 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,  是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若
 时从区间
时从区间 上任取的一个数,
上任取的一个数,  是从区间
是从区间 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x),在(0,+∞)内是减函数,又有f(3)=0,则xf(x)<0的解集为( )
A.{x|﹣3<x<0或x>3}
B.{x|x<﹣3或0<x<3}
C.{x|﹣3<x<0或0<x<3}
D.{x|x<﹣3或x>3}
相关试题

